ランニング効率化の鍵:体重移動を組み込んだら、ある意外な変化が!
今回は体重移動の話です。
これまでは接地点というのは、大きさを持たない点を想定していました。この点を接地するかしないかという区別だけでした。接地しているときには地面からの反力を得られますが、接地していないときには身体重心に力を作用させることはできません。人間の場合には、足裏という広がりがあります。そして、足裏の範囲において体重移動をします。この体重移動をシミュレーションに組み込んでみました。
- 平均速度Vが5.0 m/sにおいて、重心移動距離fが0.05 mのときに全体の仕事Wが最小値を示した。しかし、僅かな差であった。
- 着地の瞬間の仕事率を比較したところ、重心移動距離fが0.04 mのときに約12%の減少が見られた。体重移動を行うことで、着地時に瞬間的に発揮する力を削減できることが示された。
シミュレーションの方法
従来の接地点を接地点1とします。接地点1から重心移動距離fだけ前方に新しく接地点2を設けました。重心移動距離fを変えて、最適値を探ります。体重移動に関する基本的な考え方は以下の通りです。
- 接地点1のみで運用すると、身体重心との距離の上限に到達したら離地するしかありませんが、接地点2は接地点1よりも前方に位置するため、接地点2に乗り換えて接地し続けることができます。つまり、その分だけ長く接地することになります。
- 着地の瞬間は接地点1のみが接地します。したがって、従来のシミュレーションと変わりはありません。
- 着地の瞬間の身体重心との距離と身体重心との距離の上限Hとの差に対する比率に比例して、接地点1から接地点2に体重移動していきます。着地の瞬間は接地点1が100%ですが、身体重心と接地点1の距離がHに到達したときには接地点2が100%になります。中間では両者の加重平均となります。また、身体重心と接地点1の距離がHを超えた後は接地点2が100%のままとします。
- 身体重心と接地点2の距離がH+fに達したときには接地点2が離地します。
- 離地の瞬間は接地点2のみが作用します。このとき、接地点2と身体重心を結んだ線の垂直からの傾きをθ’2とします。
- 脚の重心は着地の瞬間には、接地点1と身体重心を結んだ線分の中点に位置することとします。離地の瞬間には接地点2と身体重心を結んだ線分の中点に位置することとします。中間では接地区間における身体重心の移動距離の比率による加重平均とします。
体重移動の本質を確認する
ところで体重移動とは物理的には何を意味しているのでしょうか。足裏の範囲内で体重を動かすと言っても、静止状態でなければ、身体重心の直下が体重の位置ということはありません。そもそも両足で立っているときには、身体重心の直下は両足の間になりますから、足裏の範囲外です。接地点が面積を持たない点であれば、起こり得ない論点ですが、接地点が片脚につき2つになると、それらの間で体重移動が可能になります。したがって、上記の問いに対して、物理的な解説を示しておこうと思います。
着地の瞬間
従来のシミュレーションと同じです。踵の位置にある青い星が接地点1を表しています。つま先の位置にある白い星は接地点2を表しています。接地点1からだけベクトルが出ています。接地点1のみが接地しており、地面から反力を受けているということを示しています。ベクトルの作用線は身体重心を通りますので、重心に対してそのベクトルが作用していることと同じです。
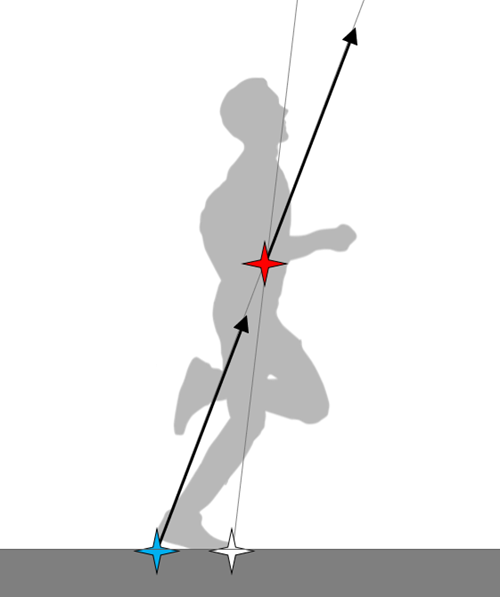
着地の直後
接地点2(つま先にある水色の星)からも小さなベクトルが出ています。つまり、接地点2にも地面から反力を受けています。ただし、接地点1(踵にある水色の星)に比べて小さいです。2つのベクトルはそれぞれ作用線の原則に従い、身体重心に向かっています。したがって、重心に作用する2つのベクトルとして、合力を作図してみると、身体重心から伸びる黒い大きなベクトルになります。この作用線が地面と交差する位置(青い星)を見ると、接地点1よりもわずかに前方になります。つまり、この青い星の位置から、合力と同じベクトルの反力を受けたのと同じであるということです。

中間点
接地点1と接地点2からほぼ同じ大きさのベクトルが伸びています。これら2つのベクトルを身体重心の位置で合成します。すると、接地点1と接地点2のほぼ中点から地面反力を受けているのと同じ状況であることがわかります。
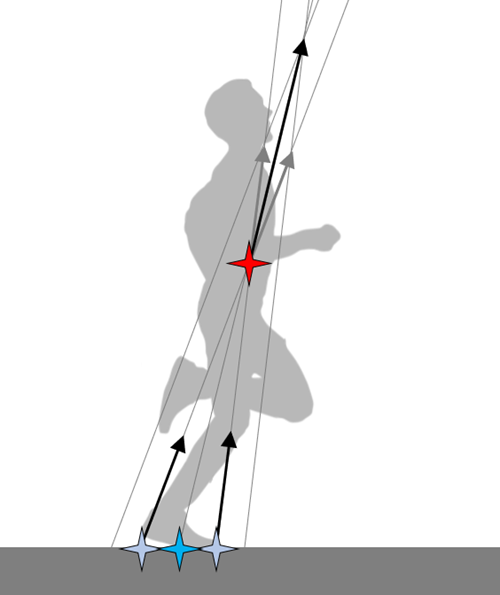
このように、接地点1と接地点2で受ける地面反力の大きさ(ベクトルの長さ)に応じて、あたかも接地点1と接地点2を結ぶ線分上のどこかで地面反力を受けた場合と物理的に等価の状況になるのです。接地点1と接地点2の地面反力の大きさの比が2:1であるなら、接地点1から接地点2へ1/3進んだ位置で地面反力を受けたことと物理的に同じなのです。こうして、接地点1と接地点2において受ける地面反力の比率が変化することで、あたかも地面反力を受ける点が2つの離れた接地点の間を連続的に移動することを、体重移動と呼んでいるのです。接地点1と接地点2においてそれぞれ受ける地面反力の比は、人間であれば足首関節の伸展によって調整することができます。
シミュレーションの結果
平均速度Vは5.0 m/sとしました。1キロ3分20秒です。体重移動距離fを0から0.06 mまで変化させながら、全体の仕事量Wが最小となるように計算を行いました。ただし、体重移動距離を含めるに当たって、身体重心と接地点の距離の上限Hを1.1 mから1.0 mとしました。身長170 cm、体重60 kgという設定において、上限Hを1.1 mとしていたのは、離地の瞬間には足首関節を伸ばすことを想定していたためです。今回のシミュレーションでは、足首関節の動き自体を最適化するため、足首関節の伸展を除いて、上限Hを1.0 mとしました。
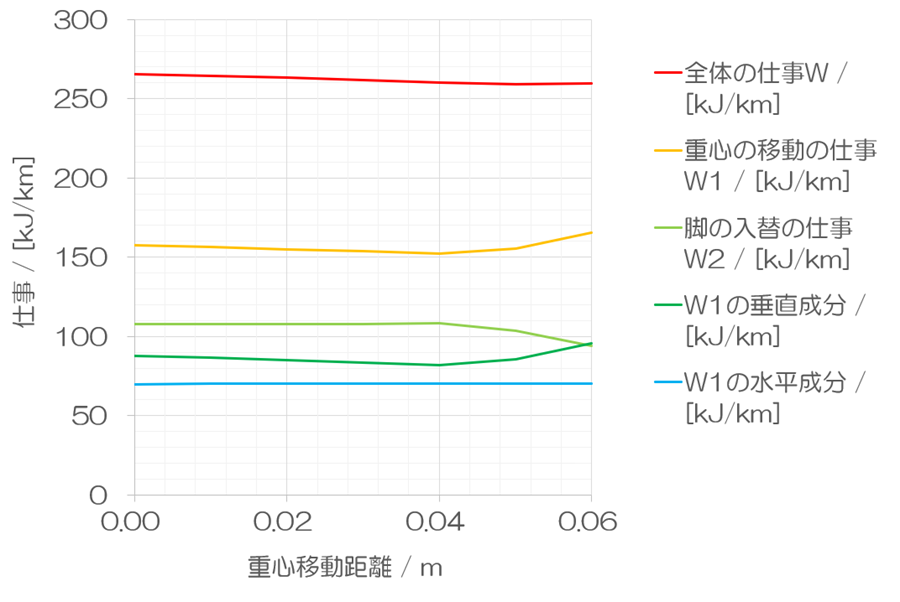
仕事
全体の仕事Wが体重移動によって減少するかどうかは最も重要な指標です。体重移動距離fが長くなると、0.05 mまでは全体の仕事Wが減少しました。と言っても、ほんのわずかな変化です。しかし、重心移動の仕事W1と脚の入替の仕事W2は0.04 m以降で明らかに変化しています。W1は増加し、W2は減少します。しかし、それらの増加と減少がほぼ完全に相殺するため、全体の仕事Wの変化が微小になっているのです。したがって、0.04 mを境にして何かが変わることは読み取れます。また、わずかな差とは言え、体重移動距離fが0.05 mのときに、全体の仕事Wが最小値を取りますので、体重移動距離fは0.05 mが最適というのが、とりあえずの結論です。
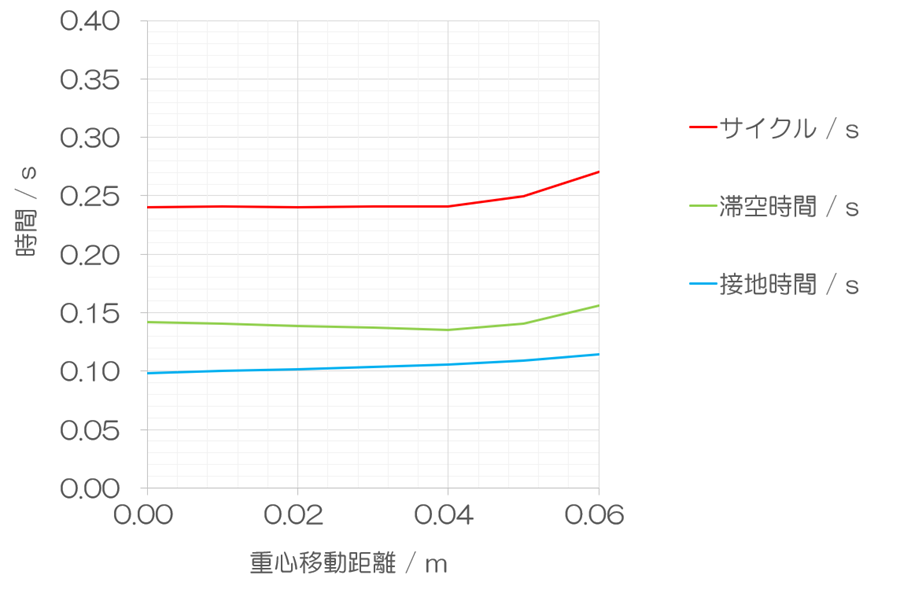
ストライドとピッチと滞空時間
グラフ作成の都合上、ピッチはサイクルで示してあります。ピッチ(歩/min)で見たい場合は、テーブルを参照してください。サイクルは、体重移動距離fが0.04 mまで緩やかに延長し、その後は急激に延長します。滞空時間は0.04 mまで緩やかに短縮し、その後は延長に転じます。接地時間は、体重移動距離fの延長と共に単調に延長します。
これら3つを総合すると、fが0.04 mまでは滞空時間が短縮し、接地時間が延長することから、サイクルは延長してもピッチ走法の範疇にあると考えます。しかし、0.05 mからは滞空時間とサイクルが大きく延長し始めることから、ストライド走法に切り替わったと考えます。体重移動距離が加算されることにより、ストライドが拡大し(=サイクルが延長)、接地時間も延長しました。
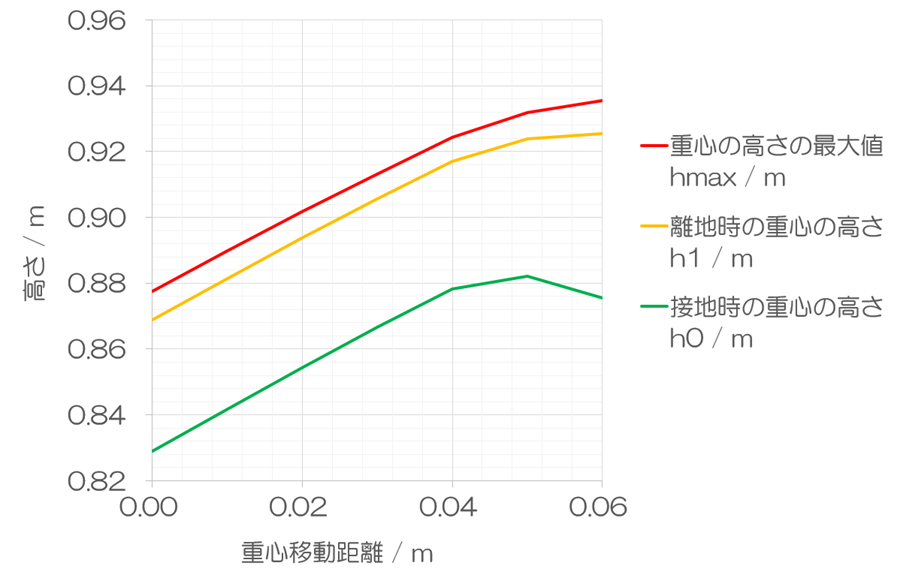
重心の高さ
体重移動距離fが大きくなることにより、重心の高さの最大値hmaxと離地時の重心の高さh1は単調に高くなります。一方で、着地時の重心の高さは体重移動距離fが0.05 mのときに最大値を取り、その後は低下します。0.05 mまでの傾向は、接地点1と接地点2が分離することで、体重移動距離の分だけ脚が長くなったのと同じような効果が表れます。同じ速度であれば、体重移動距離fが長くなるほど、離地時の身体の傾きθ’2は小さくなります。つまり、身体重心は高くなります。しかし、0.05 mよりも大きくなると、状況は変わります。ストライドが大きい走りに切り替わります。滞空時間が長くなるため、着地時の重心の高さh0は低下します。
着地時の仕事率
体重移動距離が長くなる過程において、ランニングに様々な変化が起こることがわかりました。しかし、全体の仕事Wについては実質的には変化がありません。そうであるならば、体重移動は不要であるという結論にしか至りません。これまで、ランニングの効率は、仕事を基準に考えてきました。1kmを走るときに仕事が小さい方が効率的という指標です。これは間違ってはいませんが、明らかに指標の全てではありません。検討を重ねる中で、仕事という指標では実質的に差がないところまで、最適化が進行したのです。
そこで、一旦、お蔵入りにしておいた筋出力の最大値という項目に再注目しました。重力ランニングの理論構築の初期の段階において、ランニングの速度を制約するのは筋力の最大値であることは既に指摘していました。その後は、長距離走を想定し、最高速度より確実に小さい、一定の速度で運行する際の筋力は十分に賄えるものと仮定していたため、出番がありませんでした。
重力ランニングのシミュレーションにおいて、筋出力が最大になるのは、間違いなく着地の瞬間です。シミュレーションは現在、接地区間と滞空区間のそれぞれを200フレームに分割して計算しています。着地の瞬間を意味する1フレームにおいて、重心の落下の運動エネルギーを相殺し、また、重心の高さを接地区間全体で回復するための垂直方向上向きの速度を発生させるだけの力を発生させています。それ以降のフレームでは、身体重心に作用する重力を相殺する力を割り当てているに過ぎません。着地の瞬間に得た、垂直方向上向きの速度によって、離地する瞬間までに淡々と高さを回復させていくのです。
ただし、力だけでは比較できません。1フレームの意味する時間が条件によって変化するためです。そこで、着地の瞬間の1フレームでなされた仕事を1フレームの時間によって割り算した仕事率を、ランニング中の最大の仕事率という意味でPmaxと命名しました。最大の仕事率は、条件によらず常に着地時に発生します。ただし、この計算には、脚を身体重心に対して動かす仕事は含まれていません。地面に対して身体重心を動かす仕事のみを考慮しています。つまり、着地の衝撃を人体が受動的にいなす働きを表す指標として定義しました。したがって、仕事率が150 kW前後になっています。これは1フレームが1000分の1秒よりも短いことに起因します。現実には150 kWの仕事率は人間業ではありません。着地の瞬間の筋力を非常に短時間とした場合の計算値です。
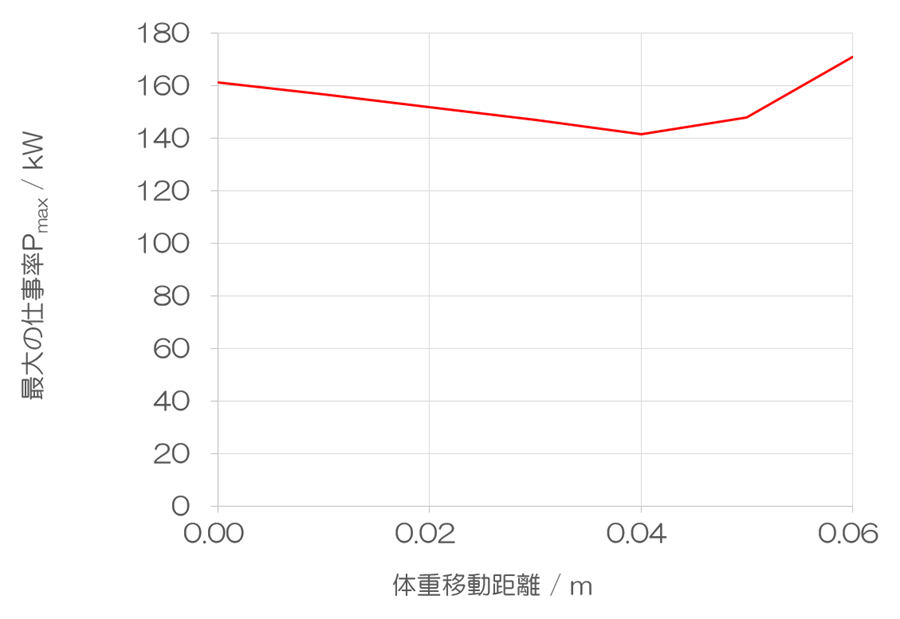
最大の仕事率Pmaxを計算してみると、期待した通りの結果となりました。体重移動距離fが0 mのときに比較して、0.04 mのときには、最大の仕事率が約12%も低下しました。12%は大きな変化です。体重移動距離が加わることにより、重心の高さの回復にかけられる距離が長くなるため、着地時に必要とされる力が小さくなるためです。そうであるならば、体重移動距離fが長くなるほどに、最大の仕事率がさらに低下するはずです。しかし、そうはなりません。0.04 mを超えると傾向が変わり最大の仕事率が上昇するのは、ストライド走法に切り替わるためであることは再三述べてきました。ただし、この切り替わりが起きる根本的な理由はわかっていません。
まとめ
今回は体重移動をシミュレーションに組み込んでみました。平均速度Vが5 m/sにおいて検証を行いました。体重移動距離fが0.05 mのときに、ランニング中の全体の仕事Wが僅かに低下しました。しかし、そのことを以て、0.05 mが最適値であると言えないほどの小さな差でしたので、別の指標として、最大の仕事率Pmaxを採用しました。体重移動距離が0.04 mのときに、体重移動しないときに比較して、約12%もの減少が見られました。
つまり、体重移動を行うことのメリットは仕事の削減ではなく、最大の仕事率の低減であるということが示されました。仕事量が大きいほど疲労を引き起こすことは自明の理だとして進めてきました。一方で、仕事量が同じ場合に最大の仕事率が高い方が疲労を引き起こすかどうかは説明を要するかも知れません。仕事量が同じということは、例えば、10 kgのダンベルを10回持ち上げる作業と、5 kgのダンベルを20回持ち上げる作業で、どちらが疲れるか、という問いです。もしも、上級者であり10 kgも5 kgも変わらないという筋力の持ち主であれば、前者と後者はあまり変わらないかも知れません。しかし、一般人であれば10 kgは最大出力に近いです。最大出力に近づくほど、最大出力に対する比率よりも、体感としては酷く消耗するという感覚は共有されていると思います。
今回は、5 m/sのみでの検証でしたが、平均速度Vを変えたら、体重移動距離fの最適値が変わることは容易に予想されます。次の記事は速度を変えて検証してみようと思います。
身体重心と接地点の上限値H:1.0 m体重:60 ㎏
片脚の質量:10 ㎏
平均速度V:5.0 m/s
オフセット:0 m
| 体重移動距離f / m | 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 |
|---|---|---|---|---|---|---|---|
| 離地時の身体の傾きθ'2 / ° | 29.4 | 29.0 | 28.6 | 28.2 | 27.9 | 28.1 | 28.9 |
| 着地時の重心の高さh0 / m | 0.829 | 0.842 | 0.854 | 0.867 | 0.878 | 0.882 | 0.876 |
| 離地時の重心の高さh1 / m | 0.869 | 0.881 | 0.894 | 0.906 | 0.917 | 0.924 | 0.925 |
| 重心の高さの最大値hmax / m | 0.878 | 0.890 | 0.902 | 0.913 | 0.924 | 0.932 | 0.935 |
| ストライド / m | 1.203 | 1.204 | 1.203 | 1.204 | 1.204 | 1.250 | 1.354 |
| ピッチ / [歩/min] | 250 | 249 | 249 | 249 | 249 | 240 | 222 |
| サイクル / s | 0.240 | 0.241 | 0.240 | 0.241 | 0.241 | 0.250 | 0.271 |
| 接地時間 / s | 0.098 | 0.100 | 0.102 | 0.104 | 0.106 | 0.109 | 0.115 |
| 滞空時間 / s | 0.142 | 0.140 | 0.139 | 0.137 | 0.135 | 0.141 | 0.156 |
| 重心の移動の仕事W1 / [kJ/km] | 157.7 | 156.5 | 155.1 | 153.7 | 152.2 | 155.6 | 165.7 |
| W1の水平成分 / [kJ/km] | 70.0 | 70.0 | 70.1 | 70.1 | 70.1 | 70.1 | 70.1 |
| W1の垂直成分 / [kJ/km] | 87.6 | 86.4 | 85.0 | 83.6 | 82.1 | 85.5 | 95.6 |
| 脚の入替の仕事W2 / [kJ/km] | 108.0 | 108.0 | 108.0 | 108.1 | 108.1 | 103.5 | 93.9 |
| 全体の仕事W / [kJ/km] | 265.7 | 264.4 | 263.1 | 261.7 | 260.3 | 259.1 | 259.6 |
| 速度の最大値Vmax / [m/s] | 5.106 | 5.105 | 5.104 | 5.103 | 5.101 | 5.105 | 5.116 |
| 速度の最小値Vmin / [m/s] | 4.932 | 4.932 | 4.933 | 4.933 | 4.934 | 4.932 | 4.925 |
| 最大の仕事率Pmax / kW | 161 | 157 | 152 | 147 | 141 | 148 | 171 |



“ランニング効率化の鍵:体重移動を組み込んだら、ある意外な変化が!” に対して1件のコメントがあります。