重力ランニングの最大の弱点を克服した話
前回の記事では、体重移動を前提として、ランニングの違いをアニメーションにより明らかにしました。体重移動があってもなくても、両方ともランニングとしては成立していると思っていたのですが、徐々にある部分が気になってきました。
それは着地した後に、重心の軌跡が急激に上昇に転じることです。着地の際に非常に大きな力が発生しなければ、このような変化は起こりません。現実の世界では、着地した瞬間に身体を持ち上げるように地面を強く蹴るということはできます。しかし、それは重力ランニングの原則からは外れているのです。自分のランニングを振り返ってみても、身体への負荷を低減するため、着地のときの衝撃を和らげるように腐心しているのです。このため、そのアニメーションを見たときに自分の中で違和感が残るようになったのでしょう。
- 耐衝撃時間(着地の衝撃に対し受動的に発揮される筋力が継続する時間)をおよそ10倍に延長することにより、着地反射筋力(着地の衝撃に対し受動的に発揮される筋力)を1桁小さくすることに成功した。
- 着地後に身体重心が上昇するまでに遅れが生じ、現実の状況に近づけることができた。
- さらに、全体の仕事Wも約14%削減することができた。
課題は一体何か?
実際、これまでのシミュレーションでは着地の瞬間に大きな力が生じていたのです。シミュレーションでは接地区間と滞空区間のそれぞれを200フレームに分割して計算しています。着地の瞬間を意味する1フレームにおいて、重心の落下の運動エネルギーを相殺し、また、重心の高さを接地区間全体で回復するための垂直方向上向きの速度を発生させるだけの力を発生させています。
これを着地の衝撃をいなす身体の能力と説明して、存在を許して来ました。現実の世界において、これに類する能力は存在します。SSC(ストレッチ・ショートニング・サイクル)=伸張反射がそれに当たります。SSCのような不随意の筋出力によって、人間は意識せずに着地の衝撃をいなして、走動作を成立させているのです。この筋出力を着地反射筋力と呼ぶことにします。
これを是とした場合でも、最大の仕事率が150 kWを超えているのは行きすぎです。重力ランニングの妥当性に関して、現状、最も疑念を呈したくなるような点であると認識しました。そこで、これを解決することを次の課題としました。
シミュレーション方法の改善
今回の検討は実にシミュレーション自体の問題点を解決することです。したがって、シミュレーションに興味のない方は、この段落は飛ばして結論だけを読んでください。
まず、着地反射筋力を、どんな場合でも1フレームに押し込めているのを止めることにしました。着地の瞬間は短いと言っても、報告されている地面反力の継続時間は0.01 sのオーダーです。身体重心の高さを回復するために必要な力積は一定と考えると、例えば、着地反射筋力を2フレームに分担させれば、最大の仕事率は半分になります。10フレームなら、10分の1です。身体への負担が劇的に削減されます。上記方針の元、作用を分担するフレーム数を1から200まで増やしてみました。接地区間のフレーム数が200ですから、分担するフレームが200とは接地区間全体で分担するという意味です。
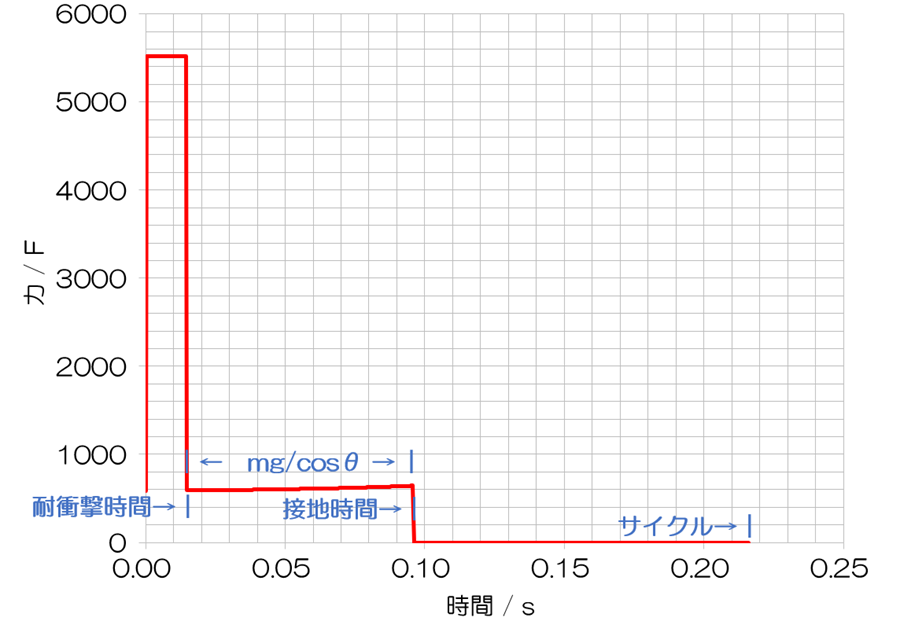
これが、ランニング中の出力の模式図です。縦軸は筋出力、横軸は時間を表しています。グラフの示す通り、本シミュレーションでは二段階の筋出力を典型としています。時間0 sが着地の瞬間です。直後に着地反射筋力を発揮します。これが続く時間を耐衝撃時間と呼ぶことにします。着地反射筋力と耐衝撃時間の積は一定としていますので、耐衝撃時間に対して着地反射筋力は反比例します。その後、重力ランニングの原則の通り、mg/cosθの筋力を発揮します。それは離地するまで継続します。
ただし、分担するフレーム数を変えた後、全体の仕事Wを最小化すると、サイクルやストライドなど全てのパラメータが変わります。したがって、フレーム数を増加させたとき、耐衝撃時間に対して着地反射筋力が反比例で減少するだけではなく、接地時間やサイクルも変化することになります。
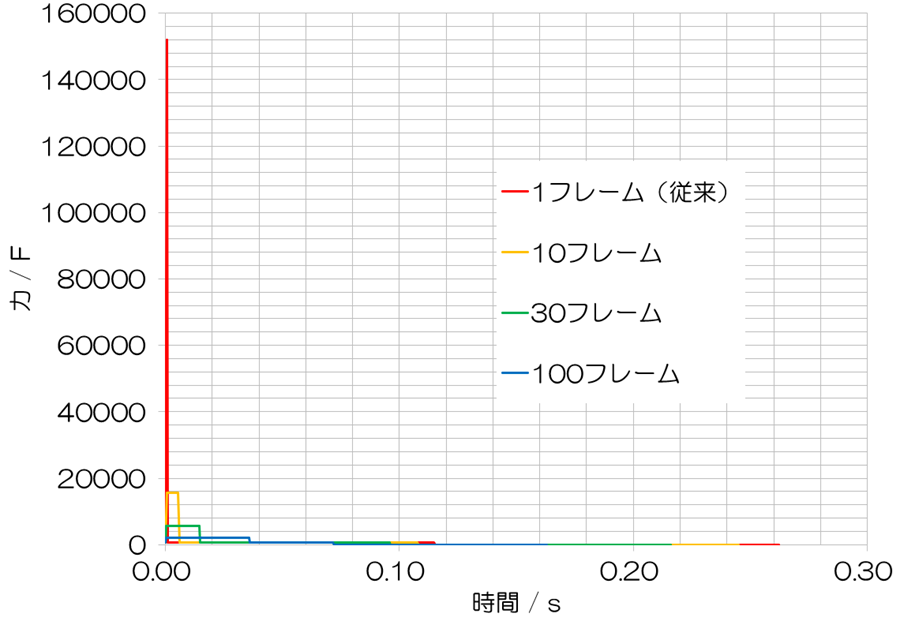
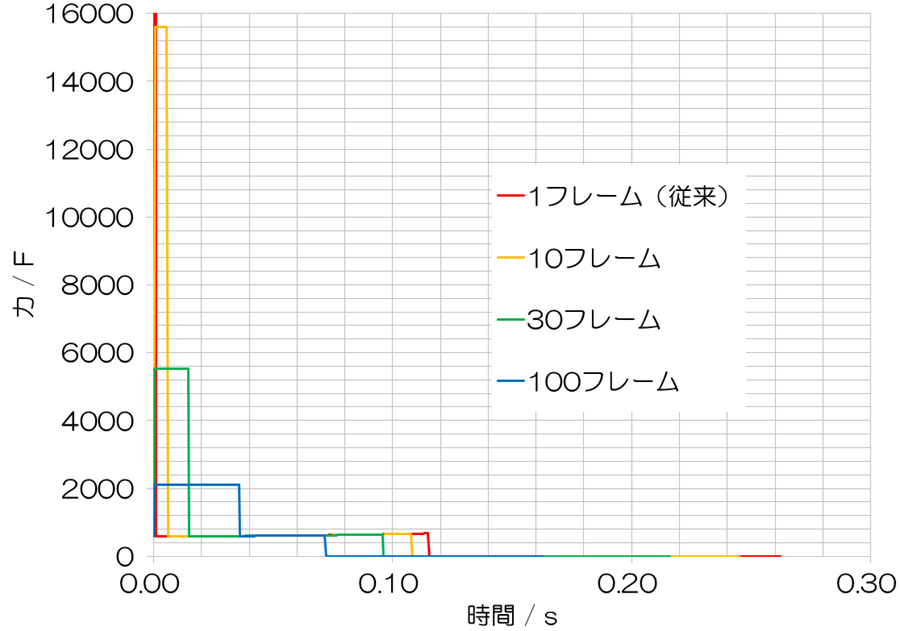
シミュレーションの結果
仕事
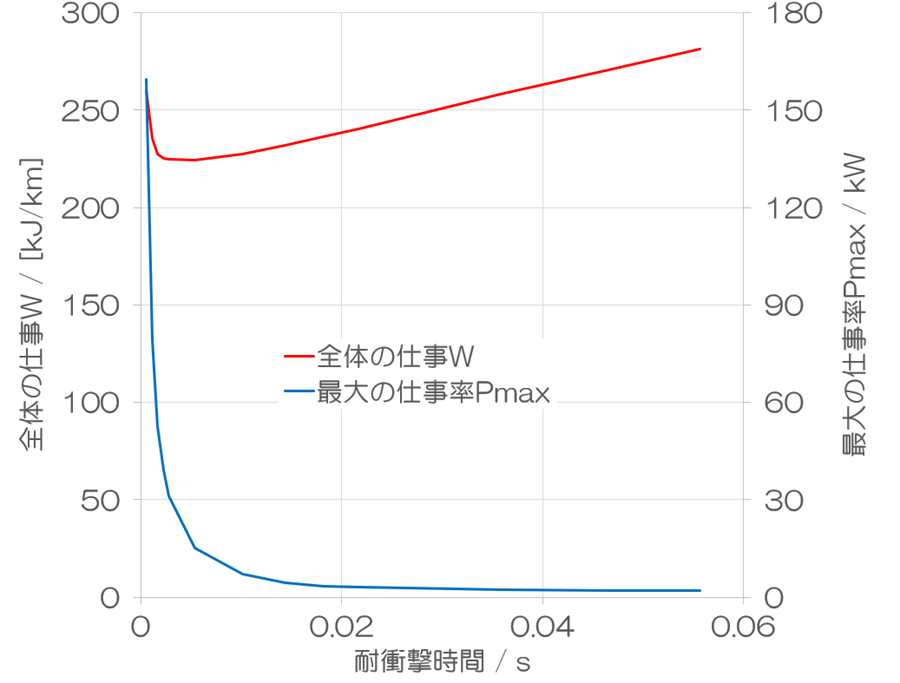
まずは、いつもの通り、仕事について見てみましょう。結論から述べると、耐衝撃時間が10フレームのときに最小値を示しました。その後は、耐衝撃時間が延長するにつれて単調に全体の仕事Wが増加していきました。一方で、全体の仕事Pmaxは耐衝撃時間に対して、おおよそ反比例の関係を示しました。耐衝撃時間が10フレームのときには、1フレームのときの約9%の値を示しました。当初、想定した通りに、着地反射筋力を1桁小さくすることができました。ここからは、10フレームのときを最適値として比較を進めます。
身体重心の動き
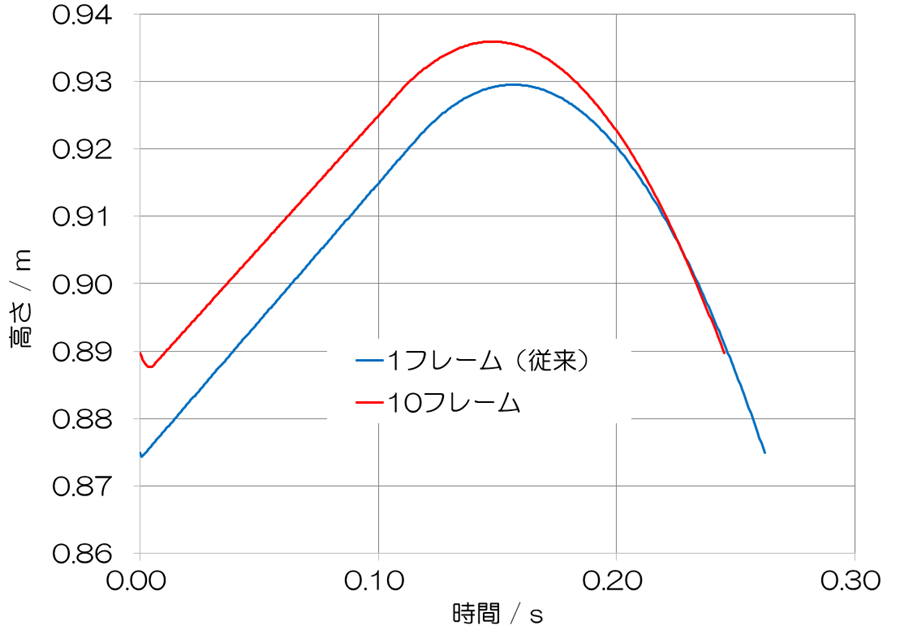
第一の目的は先述の通り、着地時における不連続な身体重心の上昇を無くすということでした。そこで、身体重心の高さを見てみましょう。耐衝撃時間が1フレームの場合は、着地後に突然、身体重心の上昇が始まっています。一方、耐衝撃時間が10フレーム(0.005 s)になると、着地直後に身体重心が上昇するのではなく、0.005 s後に上昇を開始します。グラフ上でも着地後に身体重心が下降していることが読み取れます。これが現実のランニングの動きに一致するとは思いませんが、私が不自然に感じた部分に一定の対応はなされました。
脚の運び
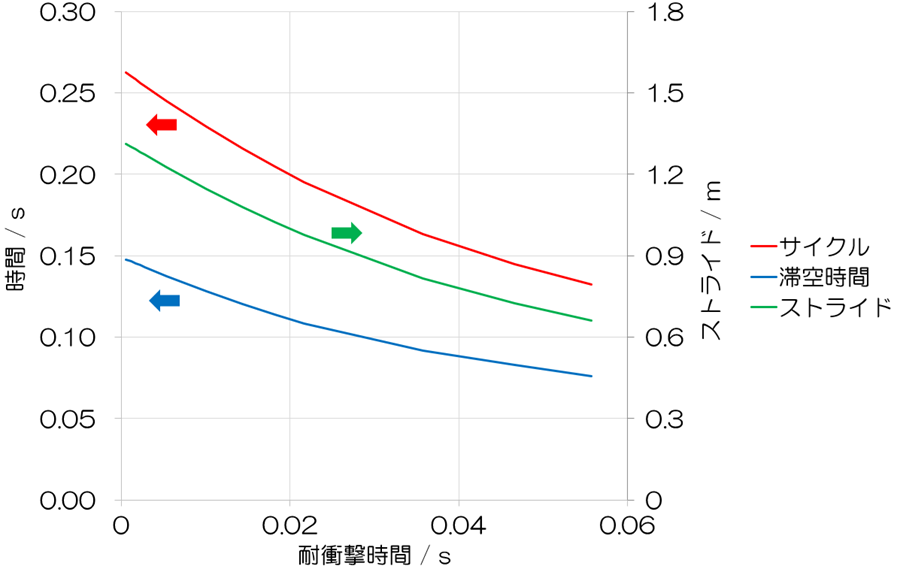
耐衝撃時間が延長するに従い、サイクルと滞空時間が短縮し、ストライドも短くなりました。傾向は単純です。脚の入替を素早く行なう方向に単調に変化しています。
重心の高さ
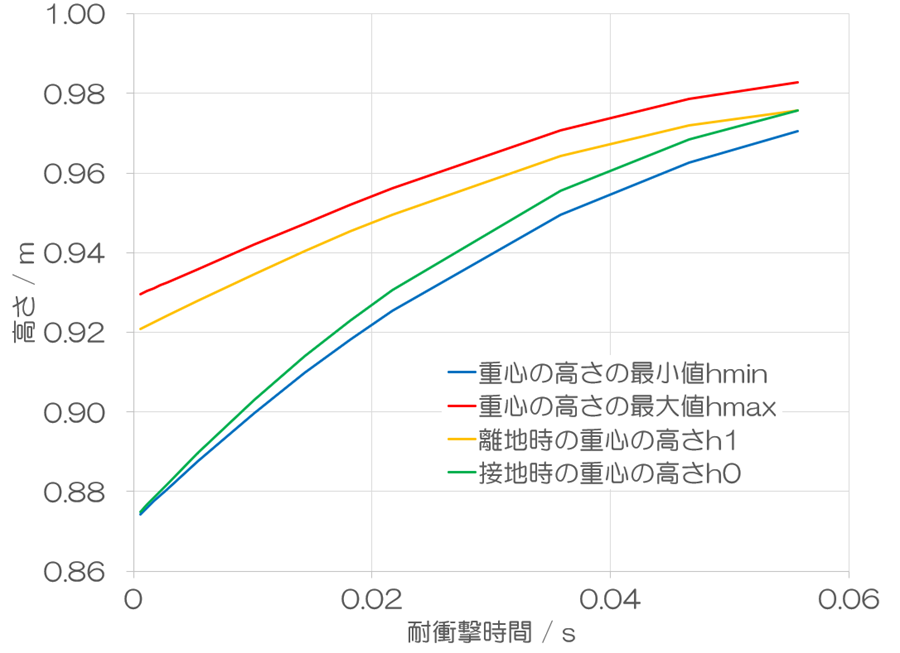
このときの重心の高さの変化も見てみましょう。耐衝撃時間が延長するに従い、全体的に重心の高さが上昇します。滞空が短くなるため、重心の高さの最大値と最小値の差はどんどん小さくなります。一方で、着地時の高さh0と最小値hminは徐々に乖離していきます。耐衝撃時間が長くなることで、身体重心が上昇し始めるまでに遅れが生じます。この間に身体重心が降下するため、両者の差が開きます。
身体重心と接地点の上限値H:1.0 m体重:60 ㎏
片脚の質量:10 ㎏
オフセット:-0.005 m
体重移動距離:0.055 m
平均の速度V:5.0 m/s
| 耐衝撃時間 / ms | 0.57 | 1.14 | 1.69 | 2.24 | 2.78 | 5.38 | 10.12 | 14.35 | 18.18 | 21.68 | 35.79 | 46.61 | 55.70 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 離地時の身体の傾きθ'2 / ° | 29.0 | 28.8 | 28.5 | 28.3 | 28.1 | 27.2 | 25.4 | 23.9 | 22.6 | 21.5 | 17.2 | 14.4 | 12.7 |
| 着地時の重心の高さh0 / m | 0.875 | 0.877 | 0.878 | 0.880 | 0.882 | 0.890 | 0.903 | 0.914 | 0.923 | 0.931 | 0.955 | 0.968 | 0.976 |
| 離地時の重心の高さh1 / m | 0.921 | 0.922 | 0.923 | 0.923 | 0.924 | 0.928 | 0.935 | 0.940 | 0.945 | 0.950 | 0.964 | 0.972 | 0.976 |
| 重心の高さの最大値hmax / m | 0.929 | 0.930 | 0.931 | 0.932 | 0.932 | 0.936 | 0.942 | 0.947 | 0.952 | 0.956 | 0.971 | 0.979 | 0.983 |
| 重心の高さの最小値hmin / m | 0.874 | 0.876 | 0.878 | 0.879 | 0.881 | 0.888 | 0.900 | 0.910 | 0.918 | 0.925 | 0.949 | 0.963 | 0.970 |
| ストライド / m | 1.31 | 1.30 | 1.29 | 1.28 | 1.27 | 1.23 | 1.15 | 1.08 | 1.02 | 0.98 | 0.82 | 0.72 | 0.66 |
| ピッチ / [歩/min] | 229 | 231 | 232 | 234 | 236 | 245 | 262 | 278 | 293 | 307 | 368 | 414 | 454 |
| サイクル / s | 0.262 | 0.260 | 0.258 | 0.256 | 0.254 | 0.245 | 0.229 | 0.216 | 0.205 | 0.195 | 0.163 | 0.145 | 0.132 |
| 接地時間 / s | 0.115 | 0.114 | 0.113 | 0.112 | 0.111 | 0.108 | 0.101 | 0.096 | 0.091 | 0.087 | 0.072 | 0.062 | 0.056 |
| 滞空時間 / s | 0.148 | 0.146 | 0.145 | 0.144 | 0.143 | 0.137 | 0.128 | 0.120 | 0.114 | 0.108 | 0.092 | 0.083 | 0.076 |
| 重心の移動の仕事W1 / [kJ/km] | 161.4 | 136.1 | 127.4 | 124.6 | 123.3 | 118.5 | 114.4 | 111.6 | 109.3 | 107.4 | 100.8 | 96.2 | 92.1 |
| W1の水平成分 / [kJ/km] | 71.7 | 70.9 | 70.7 | 70.5 | 70.4 | 70.3 | 70.2 | 70.2 | 70.1 | 70.1 | 70.1 | 70.2 | 70.2 |
| W1の垂直成分 / [kJ/km] | 89.7 | 65.2 | 56.8 | 54.1 | 52.9 | 48.2 | 44.2 | 41.4 | 39.2 | 37.3 | 30.6 | 26.1 | 21.9 |
| 脚の入替の仕事W2 / [kJ/km] | 170.1 | 170.2 | 170.7 | 171.4 | 172.1 | 175.9 | 183.5 | 190.6 | 197.2 | 203.3 | 227.7 | 244.8 | 259.6 |
| 全体の仕事W / [kJ/km] | 259.8 | 235.4 | 227.5 | 225.5 | 225.0 | 224.2 | 227.7 | 232.0 | 236.4 | 240.6 | 258.4 | 270.8 | 281.5 |
| 速度の最大値Vmax / [m/s] | 5.11 | 5.11 | 5.11 | 5.11 | 5.11 | 5.10 | 5.09 | 5.08 | 5.07 | 5.07 | 5.06 | 5.05 | 5.06 |
| 速度の最小値Vmin / [m/s] | 4.92 | 4.92 | 4.93 | 4.93 | 4.93 | 4.94 | 4.94 | 4.94 | 4.94 | 4.94 | 4.94 | 4.95 | 4.96 |
| 最大の仕事率Pmax / kW | 159.4 | 79.2 | 52.5 | 39.1 | 31.1 | 15.1 | 7.1 | 4.6 | 3.4 | 3.1 | 2.4 | 2.1 | 2.0 |



“重力ランニングの最大の弱点を克服した話” に対して1件のコメントがあります。