着地にかかる時間は一瞬?それとも長い?
前回の記事では、耐衝撃時間を最適化することで、着地の瞬間に働く仕事率を小さくすることを試みました。しかし、それでも15.1kWという値は、自転車ロードレースのトップアスリートがゴールスプリントで発生させる仕事率の約10倍のオーダーに相当します。5 msという一瞬であれば、トップアスリートの10倍の出力が発揮されても矛盾はないかもしれませんが、検証が必要であると考えています。
- 複数の文献を参照し、耐衝撃時間(着地の衝撃に対し受動的に発揮される筋力が継続する時間)を15 msとすることにした。
シミュレーションの問題点
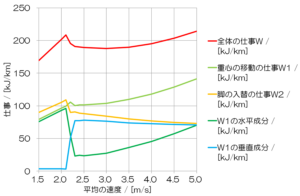
これまでの検討では、オフセットと体重移動距離は自動的に調整することができなかったため、一定の値を手動で指定していました。しかし、体重移動距離は全体の仕事Wや最大の仕事率Pmaxに大きな影響を与えるため、オフセットと体重移動距離を含めた最適化を自動化しました。これにより、速度を変更すると、ストライドやピッチと同様に、オフセットや体重移動距離も自動的に調整されるようになりました。
ただし、耐衝撃時間の自動化は簡単にはできませんでした。耐衝撃時間を延ばすほど全体の仕事Wが減少したためです。最終的に接地時間の100%を耐衝撃時間としたときに、全体の仕事Wが最小となることが分かりました。これは、重力ランニングのコンセプトとは逆で、ぴょんぴょんと跳ねるような走りでした。全体の仕事Wが最小となることが物理的に正しいとは言え、直感的に人間のランニングとしては成立しない動きであることがわかりました。シミュレーションは理論に基づいていますが、現実に即した実現可能な結果を導き出さなければなりません。この点については、論理云々ではなく、現実ありきで考える必要があります。どこが間違っていたのでしょうか。
人間の身体は非弾性体
結論から言うと、弾性体と非弾性体の違いが原因でした。これまでも論じてきたように、人間の身体の反発弾性率は0%またはそれに近い値であると私は考えています。つまり、非弾性体です。自由落下で地面と衝突しても跳ね返りません。耐衝撃時間が100%になった状態は弾性体に近い挙動に当たります。厳密には筋力の発揮が正弦波ではないため、理想的な弾性体の挙動とは異なりますが、似たようなものです。
以下の文献で示されるように、非弾性体は衝突(着地)した瞬間に大きな力が発生しますが、その後、地面に接地していても衝突の反発力は発生しません。
https://foundry.jp/bukai/wp-content/uploads/2012/07/5f8028addcf241154da042c4e03b00c4.pdf
言うまでもなく、重力は常に作用しています。したがって、衝突後は重力の反作用だけになります。一方で、弾性体の場合は、弾性変形によって長時間の反力が発生します。着地した瞬間から変形が大きくなるに従って、弾性体自身の弾性による反力が生じます。純粋な弾性体の反力は変形に正比例します。
人間の身体は非弾性体、しかも極めて低反発の非弾性体です。すなわち、着地の瞬間だけ大きな力が発生し、その後は体重を支える力だけが作用します。この体重を支える力に最小限の筋力を加えて重心を前方へ移動させるのが、重力ランニングの基本的な考え方です。決して、人間の身体を弾性体とみなして、地面に対して弾むような動きを筋力で再現しようとはしません。
したがって、耐衝撃時間が100%ということはあり得ません。正確に言うと、5 m/sという長距離走の速度ではあり得ないと考えますが、スプリントにおいては接地時間が短くなるため、耐衝撃時間が100%になる可能性もあります。これが川本さんの理論の裏付けとなるかもしれませんが、話を元に戻します。
耐衝撃時間の長さ
耐衝撃時間は、非弾性体としての人間の身体が地面に衝突したときの反力が持続する時間です。それはどれくらいの長さなのでしょうか。簡単に測定できないデータですので、インターネット上の文献を漁ってみました。
水塊の衝撃
参考になるのは以下の文献です。この研究では、水塊を落下させて平板に衝突した瞬間に生じる圧力を測定しています。最大圧力が減衰して1/eになる時間はおよそ3 msです。ただし、体積0.79L、高さ10 cmという小さな水塊の話であるため、3 msは人間の身体の耐衝撃時間としてそのまま採用するには短すぎると思います。
https://www.jstage.jst.go.jp/article/kikaic/79/805/79_3169/_pdf
粘土玉の衝撃
全く別の例ですが、粘土玉を落としたときの衝撃を測定した研究もあります。反発係数がゼロに近い粘土玉を使った場合、1 kgの粘土玉の衝撃継続時間が11 msとなっています。反発係数が1に近く非常に硬い、ボーリング玉では衝撃継続時間が1.7 msとなり、反発係数が中程度のソフトボールは2.3 msとなります。この文献では、柔らかいものほど衝撃継続時間が長くなる傾向が示されています。上記水塊の研究では、最初の衝撃が急速に減衰してからも圧力が残ります。そのため、50 msの衝撃継続時間があると言えなくもありません。水は流れやすいため、落下後に変形して散逸するまでの時間が長くなります。
https://foundry.jp/bukai/wp-content/uploads/2012/07/5f8028addcf241154da042c4e03b00c4e.pdf
人間の着地の衝撃
次に、人間の着地の衝撃についての測定値を探してみました。以下の文献では、最初のピークが約25 ms後となっています。
https://tsukuba.repo.nii.ac.jp/record/6817/files/27.pdf
また、別の文献では、Fig.4に示されるImpact peakが約40 msの継続を示しています。
https://www.sciencedirect.com/science/article/pii/S2095254617300285
これらの2つは実際の人間の着地の衝撃を測定したものです。共通点として、2つのピークが確認されます。1つ目のピークは脚が着いたときの衝撃、2つ目のピークは身体全体の重量を受けたときの衝撃です。
普通の科学的論理に従えば、実測値を基にシミュレーションを構築すべきです。実際の人間の走りを研究しているからです。しかし、もし、現行の走り方が間違っている(非効率である)としたら、そのデータを基に解析を行うことには意味がありません。私は新しいランニングモデルの提示を目指しており、実測値をそのまま取り入れることは論理破綻となると考えます。一般的に、連続跳躍が走ることだと認識されていますので、私はこれらの2つのピークが踵着地の筋肉走りを表していると解釈しました。
さらに、以下の文献も大いに参考になりました。
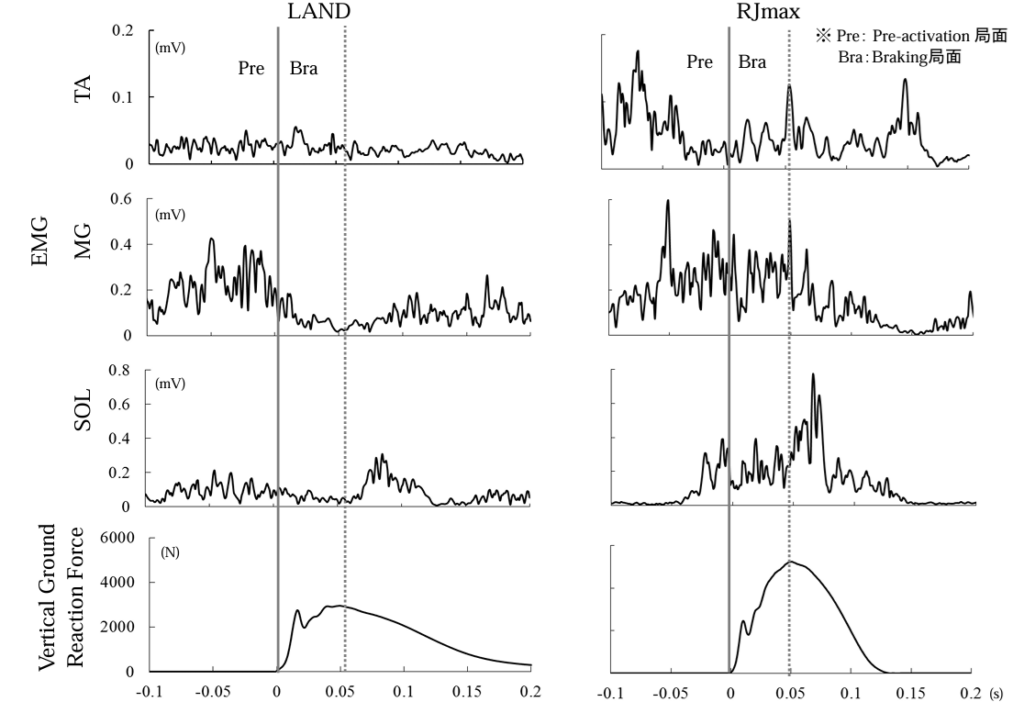
この文献のFig. 3には、所定の高さから落下して着地した場合とドロップジャンプを行った場合の地面反力の時間経過のグラフが示されています。左側が着地、右側がドロップジャンプです。両者とも2つのピークから構成されています。1つ目のピークは約15 ms後に最大値を示し、2つ目のピークは約50 ms後に現れます。2つ目のピークは着地の場合に比較して、ドロップジャンプの場合には2倍程度の高さとなっており、随意の筋力の影響であることがわかります。
また、着地時の地面反力のピークは数千Nのオーダーとなっており、重力ランニングのシミュレーションの耐衝撃時間に発生する筋力と同じオーダーになっています。耐衝撃時間を1フレームに限定せずに、拡張していくことを支持する結果となっています。
考察
私の試みは、実際の人間の走りを測定してシミュレーションで再現することではなく、身体重心に作用する力を重力と筋力と空気抵抗に限定し、演繹法的にランニングの本質を炙り出すことです。ゆえに、1つの点である身体重心に対する力の作用だけを考慮しているため、シミュレーションにおいて反力のピークが2つに分かれることはありません。また、身体の部位ごとの動き(ふくらはぎの筋肉など)も考慮していません。そのため、仮想的な緩みを導入することで耐衝撃時間を延ばすことをシミュレーションに組み込みました。
人間の身体を1つの塊として捉えた場合、適切な耐衝撃時間はどれくらいでしょうか。0.79Lの水塊の耐衝撃時間が3 msであるならば、人間の身体はずっと大きいため、耐衝撃時間は長いと予想されます。また、人間の身体は7割が水ですが、水のように流れるわけではありません。骨と筋肉によって支えられ、一定の形を保つことができます。ただし、筋肉によって支えられていても、一定の緩みがあります。この緩みの程度が大きいほど、耐衝撃時間が長くなると考えられます。
これらを考慮し、ドロップジャンプの文献の1つ目のピークが約15 msで極大値を迎えることから、耐衝撃時間は15 msにしようと思います。現実の人間の身体は複数の部位が連結した構造体ですので、1つの塊としての応答は、1つ目のピークと同じ時間に現れるのが妥当です。2つ目のピークの極大値を迎えるまで50 msは長すぎると考えます。この時間は人間の身体が着地後に、随意的に地面を蹴ろうとするときの準備の時間であり、1つの物体の衝突による反力の発生ではないと考えました。
重力ランニングのシミュレーションでは、耐衝撃時間において落下の運動量を完全に相殺し、さらに、身体重心の高さを接地時間のうちに回復する垂直方向上向きの速度を付与します。その後は、身体重心の垂直方向の速度が変化しないように、最低限の地面反力を得るための筋力を発揮します。つまり、接地時間のうち最初の15 msを耐衝撃時間とし、その後の時間は接地時間により変化します。ランニング中の地面反力は、非弾性体のように着地の瞬間に大きな反力が発生し、その後は重力の反作用だけ(地面を全く蹴らない)になる、というのが私の理想であり、現在のランニング中の感覚です。
長くなりましたのでシミュレーションの結果は別の記事にします。