物理モデルの再構築:重力ランニングと筋力走りの統合的理解に向けて
筋肉走りのモデル化における困難
筋肉走りと重力ランニングの比較を行おうとしました。筋肉走りの物理モデルを作成して、重力ランニングのそれと比較しようとしました。ところが、筋肉走りの物理モデルの作成は難しいということがわかりました。重力ランニングのモデル化は、無駄を省いていく作業です。したがって、一定の目的地を設定し、距離を縮めて、向かっていくようなものです。
一方で、筋肉走りは無駄を追加する作業です。これは今、目的地にいるのに、そこから離れて歩くようなものです。どちらへ向かっても良いのですが、いずれにしても無駄であることには変わりありません。そうすると、どうしたら良いのかが決められないのです。何らかの無駄を付け加えたモデルを作るのですが、どのような無駄が合理的に、筋肉走りと認められるものかを考える必要があります。
筋肉走りのモデルを作ろうとすると、重力ランニングにおいては固定されていた要素を動かすことになり、これを許容するシミュレーション方法を作らなければなりません。新しいシミュレーション方法において、まずは、重力ランニングを表現してみることにしました。最適値の存在する重力ランニングを表現してみてから、無駄を付け加える(筋肉走り)とどうなるかを表現するためです。
- 筋肉走りのシミュレーションを試みる中で、汎用的なシミュレーションの方法を組み立てる必要が生じた。この方法で、重力ランニングを表現したところ、滞空中の上昇は避けられないことが判明した。
- この変更により、物理モデルの定義においては、筋肉走りと重力ランニングの明確な区切りを定義することはできなくなった。
重力ランニングのモデルは以下のような前提によって成り立っています。
- 筋力Fを一定のルールの元に発生させる。
- 筋力Fの作用線は接地点と身体の重心を常に通る。(重心作用線の原則)
- 身体の重心には常に重力が作用している。
- 筋力Fと重力が身体の重心に作用することにより、重心の速度Vが変化する。
- 速度Vにより身体の重心が移動し、身体の重心の座標(x,y)が変化する。
- 力Fを水平成分Fxと垂直成分Fyに分解する。速度Vも同様に分解する。
a.とb.を除けば、当たり前のことを言っているだけです。物理法則に従っているだけなのです。b.もランニングの原則ですから、重力ランニングの独自性が現れるのは、a.だけです。
重力ランニングの筋力Fの発生のさせ方に本質があるのです。これも当たり前のことです。人間が制御できるのは、自分の筋力だけであり、物理法則は変えられません。
ここで言う筋力とは地面に対する作用です。したがって、接地しているときにしか発揮されません。また、方向と向きは決まっています。重力ランニングにおいては、重心に対して、mg/cosθの力を作用させます。ここで、mは身体の質量、gは重力加速度、θは垂直からの作用線の傾きです。
重力ランニングの物理モデルの修正
従来はここまででした。ところが、見直すと今まで考慮していない部分がありました。以下の2点です。
1. 接地してから離地するまでの間に重心を元の高さまで持ち上げ、かつ、離地する瞬間に重心は水平方向に運動していることになっている。しかし、接地している間には、一定速度で重心が上昇しているのだから、離地の瞬間にも重心の垂直方向上向きの運動エネルギーは存在しており、離地の直後も上昇を続けるはずである。
この点、重心を持ち上げるための仕事としては計上していました。したがって、着地した瞬間から離地した瞬間の間に、重心が獲得した位置エネルギーの分だけ仕事を行ったことは、仕事Wに含まれています。離地した瞬間の運動エネルギーが残っていることから、実際にはこの運動エネルギーの分だけ、離地後に重心が上昇してから落下が始まります。離地後の上昇は想定していませんでした。
接地している時間で重心を持ち上げつつも、離地の瞬間に向けて、筋力を小さくしていけば、離地の瞬間に、重心の上昇はゼロにすることができると考えていました。ところが、実際にシミュレートしてみると以下の2つの試行により、それは実現できないことが示されました。
・重心の上昇の運動エネルギーが当初の重心の高さの回復に足りることがわかった時点で、筋力の発揮を停止すると、重心の高さは回復するが、それは離地後に実現する。つまり、離地してからも重心の上昇は続く。
・離地の瞬間に上昇の運動エネルギーがゼロになるように、上昇の途中で筋力の発揮を停止すると、重心の高さが当初の高さまで戻らないまま、落下の局面に入る。
これらは、接地の瞬間のθは0°、また、重心の高さの上昇は一定速度で行うという前提の元での結論ですが、ともかく、離地が先で、落下の開始はその後、ということが確定しました。重心の高さ回復の後半は滞空状態にならざるを得ないのです。
要約すると、私は離地の瞬間には重心は水平方向に動いていると考えていたが、それは不可能だったというだけです。従来のシミュレーションでは、離地すると同時に落下が始まると想定していました。しかし、上昇の途中で離地し、滞空に入りますが、しばらくは上昇が続くということです。新しい方法の上昇から下降に転じる点、つまり、重心の高さの極大点を従来のシミュレーションにおける離地の瞬間と考えれば、残るのは概念上の区切りの問題だけなのです。
すなわち、重力ランニングにおいて、離地後に重心の上昇局面が存在するということを受け入れた場合には、筋力走りとの明確な区別が無くなります。
2. 着地の瞬間には、滞空中の自由落下のため、重心には垂直方向下向きの運動エネルギーが存在している。しかし、着地の瞬間に重心は落下を停止し、すぐさま、上昇に転じることになっている。重心がこのような不連続の動きをするためには、瞬間的に大きな力が加わることを意味するが、そのような力のことは考慮されていない。
この点、自由落下の運動エネルギーは仕事として計上していました。自由落下の運動エネルギーを跳躍ために再利用できるかという議論は既に行われています。このときに、反発弾性率は実質的に0%とし、散逸するものとして扱っています。したがって、ランニングエコノミーの比較という意味では、誤差はありません。
着地の際の衝撃は、瞬間的な地面からの反力です。これによって、身体の重心の落下が停止するのは確かです。したがって、この部分は着地の瞬間に落下速度を相殺するように力が発生するものとしました。この力は0.01秒間発生するものとしました。この反力が実際、筋力で発生しうるものかどうか検証されていません。
重力ランニングをより現実的に表現できた
改めて、重力ランニングのシミュレーションを実施しました。このとき、脚の入れ替えにより生じる仕事W2については、ピッチとストライドだけを変更して計算しています。
今回のシミュレーションでは、力の発生から、速度が変化し、座標が変化するということをt = 0秒から0.01秒刻みで計算していきました。離地が起こるのは、接地点と重心の距離が、設定された最大値Hを超えたときです。また、着地が起こるのは、重心の高さがh0を下回ったときです。h0の値は、理論上の離地時の身体の傾きθ2と理論上の滞空時間から求められます。着地のフレームでは、下向きの運動エネルギーを相殺する力と理論上の離地時の身体の傾きθ2で求められる距離内で重心の高さを回復するための力を発生させます。前者により落下の速度を打ち消し、後者により重心の上昇を起こします。
理論上のθ2と滞空時間を設定してシミュレーションを開始するのですが、今回の方法では、必ず、差が生じます。それは、離地後に重心が上昇することに起因します。θ2と滞空時間は実際には、もっと大きくなります。特に、滞空時間は3割から5割の差が生じます。上述のようにこの差がどうしても解消できなかったため、重力ランニングの定義自体を変えることになりました。
従来は、身体を倒す角度θ2と、滞空時間を決めていました。身体を倒す角度は1°からθ2までを50分割で計算していました。離地後の滞空時間も0秒から何秒までを50分割で計算していました。このため、どのセルで何が起こるかということが決まっていました。しかし、今回のやり方ですと、どのセルで何が起こるかはパラメータを変えるごとに全て変わります。
| 速度V / [m/s] | 4.0 | 4.5 | 5.0 | 5.5 |
|---|---|---|---|---|
| 実際の離地時の身体の傾きθ2 / ° | 21.4 | 26.6 | 32.9 | 37.6 |
| 実際の滞空時間 / s | 0.156 | 0.176 | 0.181 | 0.206 |
| ストライド / m | 1.06 | 1.33 | 1.55 | 1.85 |
| ピッチ / [歩/min] | 226 | 203 | 193 | 179 |
| 身体の重心の接地時の高さh0/m | 0.97 | 0.92 | 0.85 | 0.78 |
| 身体の重心の高さの最大値hmax/m | 1.03 | 1.00 | 0.93 | 0.87 |
| 重心の移動の仕事W1/[kJ/km] | 171.6 | 183.6 | 190.6 | 206.0 |
| 脚の入替の仕事W2/[kJ/km] | 83.2 | 79.3 | 82.4 | 80.3 |
| 合計の仕事W/[kJ/km] | 254.8 | 262.9 | 273.0 | 286.3 |
速度Vを4.0、4.5、5.0、5.5 m/sになるようにして、合計の仕事Wを最小化しました。
速度が大きくなるほど、θ2が大きくなり、また、滞空時間も長くなりました。これに伴い、ストライドが大きくなり、ピッチが減少しました。これらの傾向は従来のシミュレーションと同様です。合計の仕事Wの絶対値は従来よりも大きくなりました。これは重心の上下動を正しく組み込めたことを示していると考えます。
以下に各速度における重心の挙動を示します。各シミュレーションの結果から、典型的な一歩を抜き出して表示しています。したがって、グラフが終わる点のx座標はストライドと一致します。
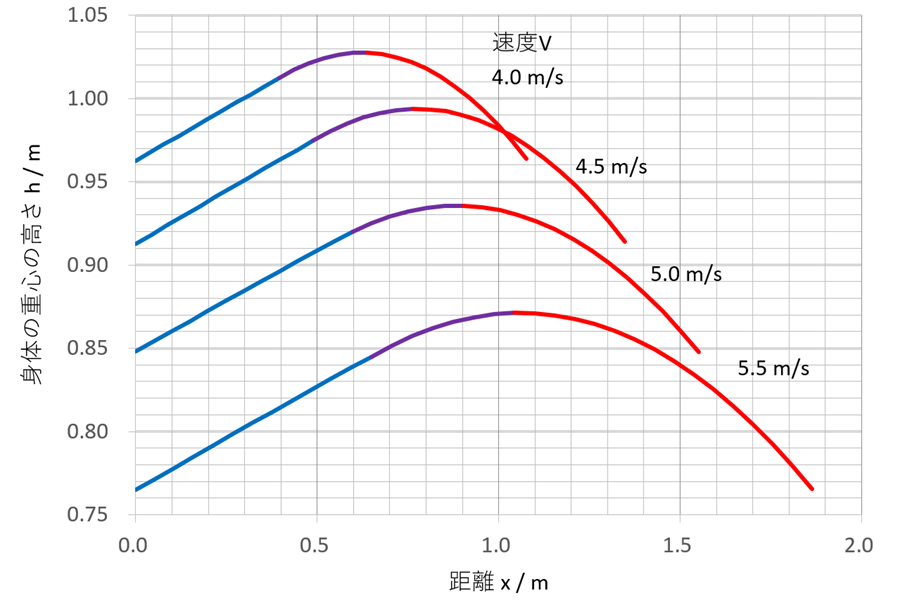
青色は接地している区間を表しています。紫色は離地後に重心が上昇している区間、赤色は重心が落下している区間です。紫色で表示している区間が今まではないものとみなしていました。青色のように直線の区間の後に、すぐ落下が始まるように計算していました。この点は、考慮不足でした。
速度が大きくなるほど、
- ストライドが大きくなります。これは当然に理解されると思います。
- 重心の高さが低下しています。これは離地時の身体の傾きθ2が大きくなっているためです。ストライドを大きく取ろうとすれば、脚を大きく開く必要があることを示しています。
- 重心の上下動が大きくなります。速度を大きくするためには滞空時間を長くする必要があります。
速度が大きくなっても、重心の上昇局面において、x座標に対するy座標の増加率は変わりませんでした。上記条件においては、各速度における曲線が相似になっているように見えます。これが、重力ランニングにおいて最適化がされているということかもしれないと思っていますが、詳しい考察は未実施です。
筋肉走りのモデル化に取り組む中で、重力ランニングの理論を修正することができました。重力ランニングにおいて、滞空時に重心の上昇局面が存在することがわかりました。筋肉走りと重力走りの決定的な違いはなくなってしまいましたが、より汎用的な方法で導かれた結論の方が、現実に近いと考えます。
次は、筋力走りに内在する無駄を合理的に定義してみようと思います。



“物理モデルの再構築:重力ランニングと筋力走りの統合的理解に向けて” に対して1件のコメントがあります。