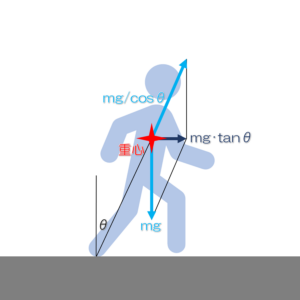
身体の傾きと走行抵抗のバランスで巡航速度が決まる
このブログでは、ランニングというワードを使っていますが、それはマラソンに代表される長距離走を主として意味しています。長距離走においては、その距離のほとんどを一定の速度で巡航します。スタート時の加速は重要ではありません。そこで、巡航時に身体の傾きがどのように作用しているかを解説します。
身体を傾けると重心に対して推進力が作用することを示しました。しかし、推進力が作用するということは加速するということです。では、人は身体を傾けていれば無限に加速していくのでしょうか。もちろん、そんなことはありません。速度が増加して行っても、その増加を維持することができずに、一定の速度へ収束していきます。
何故、そうなるのでしょうか。大きく分けると以下の2つになります。
- 速度が増加するほどに抵抗が大きくなるから。
- 速度が増加するほどに筋力が足りなくなるから。
本記事では前者について解説します。
- 走行抵抗において空気抵抗の寄与は小さい。
- 着地時のブレーキが速度を抑制する主たる抵抗になっていると推測される。
速度が増加するほどに抵抗が大きくなる
1つ目の答えは、速度が増加するほどに、抵抗が大きくなるからです。抵抗とは進行方向逆向きに働く力のことです。ランニングにおいては、通常、空気抵抗のことを指します。
重力ランニングにおいては、身体の傾きθが一定であれば、推進力も一定です。その推進力によって速度が増加していきます。しかし、速度が増加するほどに、空気抵抗が大きくなります。推進力と空気抵抗が釣り合ったところで、速度が一定になります。傾きθが大きいほどに、大きな速度で一定となることがわかります。
それを算出してみたのが以下の表です。
| θ | 推進力/kgf | 巡航速度/[m/s] | 巡航速度/[分/km] |
|---|---|---|---|
| 0 | 0.00 | 0.00 | n/a |
| 1 | 1.05 | 3.31 | 05:02 |
| 2 | 2.10 | 4.68 | 03:34 |
| 3 | 3.14 | 5.74 | 02:54 |
| 4 | 4.20 | 6.63 | 02:31 |
| 5 | 5.25 | 7.41 | 02:15 |
| 6 | 6.31 | 8.13 | 02:03 |
| 7 | 7.37 | 8.78 | 01:54 |
| 8 | 8.43 | 9.40 | 01:46 |
| 9 | 9.50 | 9.97 | 01:40 |
| 10 | 10.58 | 10.52 | 01:35 |
空気抵抗の算出には、「眠れなくなるほど面白い 図解 物理でわかるスポーツの話」の長距離の章を参考にしました。ただし、体重は60㎏としました。
この本では、速度を決めて、その速度を実現する身体の傾きを求めています。この記事では、逆に身体の傾きを変化させていき、空気抵抗と釣り合う速度を求めてみました。すると、θ=2°のときに、1キロ3分34秒の速度になりました。しかし、この傾きは現実に照らし合わせると、小さすぎると感じます。
実は、それは当然です。なぜならば、現実世界では明らかに、走行時の抵抗は空気抵抗だけではないためです。空気抵抗を含めた走行時の抵抗の全てを包括して、走行抵抗と言います。自動車業界では良く使われるワードです。ランニングにおける空気抵抗以外の抵抗として、以下のようなものがあると思います。
- 靴の反発係数が1より小さいことによるエネルギー損失
- 身体の中の液体成分の変形時のジュール熱
しかし、着地時のブレーキは走行抵抗の定義に含まれないと私は考えます。本質的に走行することによって生じるのではなく、ランニングメソッドを改善することによって低減できるためです。
参考までに、自動車において、走行抵抗に占める空気抵抗の寄与はどの程度なのかを調べてみました。以下の資料によると、空気抵抗を1とすると、その他の抵抗はおよそ1.7でした。
https://www.tokyokankyo.jp/kankyoken_contents/cmsup/pdf/houkoku203.pdf
そこで、走行抵抗は大雑把に空気抵抗の3倍にしてしまったのが以下の表です。
| θ | 推進力/kgf | 巡航速度/[m/s] | 巡航速度/[分/km] |
|---|---|---|---|
| 0 | 0.00 | 0.00 | n/a |
| 1 | 1.05 | 1.91 | 08:43 |
| 2 | 2.10 | 2.70 | 06:10 |
| 3 | 3.14 | 3.31 | 05:02 |
| 4 | 4.20 | 3.83 | 04:21 |
| 5 | 5.25 | 4.28 | 03:54 |
| 6 | 6.31 | 4.69 | 03:33 |
| 7 | 7.37 | 5.07 | 03:17 |
| 8 | 8.43 | 5.42 | 03:04 |
| 9 | 9.50 | 5.76 | 02:54 |
| 10 | 10.58 | 6.08 | 02:45 |
当然と言えば当然ですが、θ=6°のときに1キロ3分33秒となりました。この値でさえ、小さい気がするのは私だけでしょうか。もっと身体を傾けて走っているように見えます。上記算出結果と現実の乖離から言えることは、現実のランニングにおいて、以下の2つのうち一方、もしくは、両方が起こっているということです。
- 走行抵抗は空気抵抗の3倍よりも大きい。
- 着地時のブレーキが抵抗となっている。
現時点では、両者のどちらの寄与が大きいのかはわかりませんが、直感的には後者が多いだろうと推測しています。そして、改めて言うまでもなく、後者をゼロに近づけていくのが重力ランニングの物理的な本質です。