重力による加速を続けた結果、〇〇が大変なことに
これまでは、片脚が接地している状態で重心を水平方向に移動させるという条件において、力の釣り合いを議論してきました。つまり、ある瞬間だけを見ているわけで、時間の広がりはありませんでした。ここからは、一歩の接地から離地の間で起こる加速、そして、連続したランニングの描写を試みていきます。
- 重力ランニングの原則に則り、重力から最大限に推進力を得ようとして脚を接地させ続けると仮定すると、ピッチが異常に増加してしまう。
- 現実のランニングでは、両脚を地面から離し、滞空することでピッチを抑制する。滞空中は自由落下し、空気抵抗を受ける。
- 許容できる範囲でピッチを増加させながら、接地時間を長くするのが重力ランニングの最適化である。
最初の一歩で得られる加速
重力が推進力の源であることは既に理解いただけたと思います。重心にかかる重力が脚という機械によって推進力に変換されているわけです。推進力が作用することにより、重心が水平方向に加速していきます。重心が前方に進んでいるわけですから、右脚で重心を支えている間に左脚を前方に移動させ、右脚で重心を支えられなくなったら、素早く左脚を接地して重心を支える。その間に右脚を前方に移動させ(以下、繰り返し)、、、というプロセスがランニングです。
まずは、右脚が離地した瞬間に左脚が着地する、すなわち、どちらか片脚が接地している、という条件で、重力による加速を記述してみましょう。簡略化のため、着地したときの身体の傾きθ1=0°、離地したときの傾きθ2=20°とします。着地のときには、ブレーキはかからないものとします。
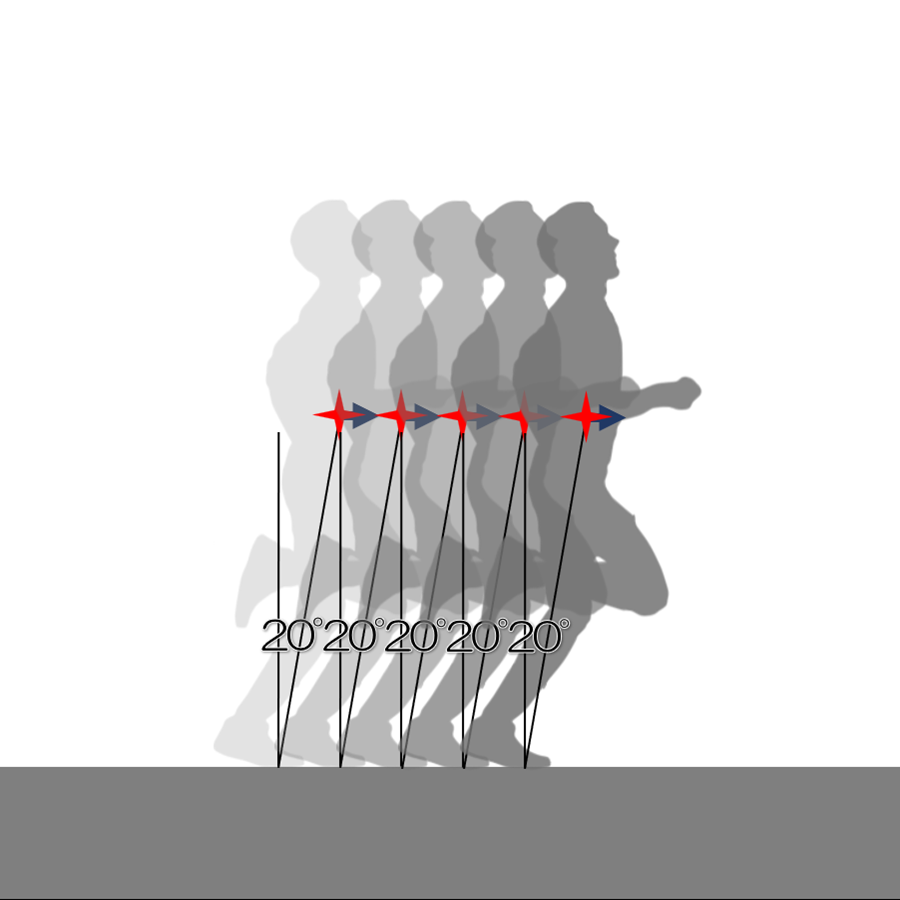
1歩目で得られる速度は、推進力Ff=mg・tanθを0°から20°まで積分することでわかります。
ここで、走行抵抗Frを空気抵抗の3倍として設定しておきます。空気抵抗の算出については「巡航速度と身体の傾きの関係1」を参照してください。
Fr=Cd・0.5・ρ・V2・A・3
すると、重心に対して前方に働く力F=Ff–Frとなります。
Kを運動エネルギー、lを走行距離とするとdK=F・dlです。
ここで、重心の高さをhとおいたとき、dl=h(tan(θ+dθ)-tanθ)です。
これを解析的に積分しようかと思いましたが、非常に複雑です。幸い、重力ランニングの説明をする分には、その必要はありません。運動エネルギーKを、θを1°刻みで計算して積算しました。
このとき、運動エネルギーK=40Jとなり、速度V=1.16m/s、走行距離l=0.36mです。重力ランニングに則って、傾き0°から20°まで一歩進むと、1.16m/sまで加速するのです。
歩数を増やしたときの結果
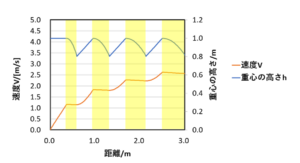
しかし、1.16m/sでは遅すぎますから、可及的速やかに加速したいところです。この条件を満たすためには、1歩目が離地した直後に、逆脚を着地して、次の一歩を開始します。次の一歩も0°から20°まで傾けることにします。2歩目における力Ffは1歩目と変わりません。Frの方は速度の項Vが含まれていますので、速度Vの二乗に比例して大きくなります。一歩の走行距離は変わりませんので、lは1歩目の倍になります。このようにして、前の一歩の直後に次の一歩を接地することで、常に片脚を接地した状態で加速していくと仮定し、計算した結果が以下の表です。
身体の傾きθの範囲:0°から20°重心の高さhの初期値:1 m
| 歩数 | 走行距離l/m | 運動エネルギーK/J | 速度V/[min/km] | 経過時間/s | ピッチ/[歩/min] |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | n/a |
| 1 | 0.36 | 40 | 0:14:21 | 0.99 | 61 |
| 2 | 0.73 | 80 | 0:10:14 | 1.27 | 219 |
| 3 | 1.09 | 117 | 0:08:26 | 1.47 | 289 |
| 4 | 1.46 | 154 | 0:07:22 | 1.65 | 342 |
| 5 | 1.82 | 189 | 0:06:38 | 1.80 | 387 |
| 10 | 3.6 | 349 | 0:04:53 | 2.4 | 545 |
| 20 | 7.3 | 597 | 0:03:44 | 3.3 | 725 |
| 40 | 14.6 | 898 | 0:03:03 | 4.8 | 896 |
| 60 | 21.8 | 1051 | 0:02:49 | 6.1 | 972 |
| 80 | 29.1 | 1128 | 0:02:43 | 7.3 | 1007 |
| 100 | 36.4 | 1167 | 0:02:40 | 8.5 | 1025 |
現時点では、まだまだ、現実のランニングを定量的に表しているとは言えません。しかし、そこから読み取れる本質もあります。重力を利用すると、わずか5秒で1キロ3分の速度まで加速していけるのです。改めて、重力の一部を変換するだけで大きな推進力が得られることが示されました。
しかし、1歩の距離が36cmで走るという仮定になっていますから、ピッチが異常に大きな値になっています。繰り返しますが、脚が接地しているときに重力の一部を推進力として利用できるので、片脚が離地したら、直後に逆脚を着くという縛りを付けました。ともかく、重力を最大限に活用するという重力ランニングの原則を守っている訳です。モーターのように回転数が0rpmから数万rpmまで、際限なくスムーズに上昇していけば良いですが、現実的には、240歩/minが限界でしょう。では、どうしたら良いのでしょうか。
ピッチを抑制するための滞空
それは、皆さんもご存じの通り、「跳ぶ」のです。ここで言う「跳ぶ」は、ただ両足が地面から離れていることを意味しています。地面を蹴って、重心を上方に上昇させることはせず、ただ、脚を地面から離すのです。これを滞空と呼ぶことにします。滞空すれば、そのまま空中を運動し続けることができます。ただし、滞空中は重心が自由落下し始めます。また、空気抵抗により速度が減少します。したがって、重心の高さhを回復させるため、また、速度Vを回復し、あるいは増加させるために、一定の時間が経過したら、再び接地することが必要になるのです。
ピッチをできるだけ増加させ、滞空時間はできるだけ短くすることが重力ランニングの目指す方向です。しかし、ピッチだけを上げようとすると無理があることは明らかです。したがって、許容できる範囲でピッチを増加させ、重力から推進力を最大限に得る(筋力を最小限に使う)ということです。
重力ランニングの逆は、ストライドを上昇させ、滞空時間をできるだけ長くするというランニングメソッドです。次のような記述がパフォーマンス向上の正しい手法として紹介されている本は多数あります。
- 筋力を鍛え、ストライドを上昇させる。
- その結果、接地時間を短くなる。
いずれ詳細に議論する予定ですが、ここまで、重力ランニングを学んできた方であれば、これが物理的に非合理であることは理解いただいたと思います。ランニングとは、地面を蹴って跳んで進むことの繰り返しではありません。両足が離れているのは、ピッチを上げられないために、仕方なく滞空しているだけなのです。この考え方の転換を行なってください。