身体の傾きを拡大するとどうなる?ランニングエコノミーの可視化の試み
身体の傾きθの範囲を拡大する
滞空時間を短くする方法は2つあります。1つは本当に滞空時間を短くする方法、もう1つは接地時間を長くする方法です。今回は後者を調査してみます。
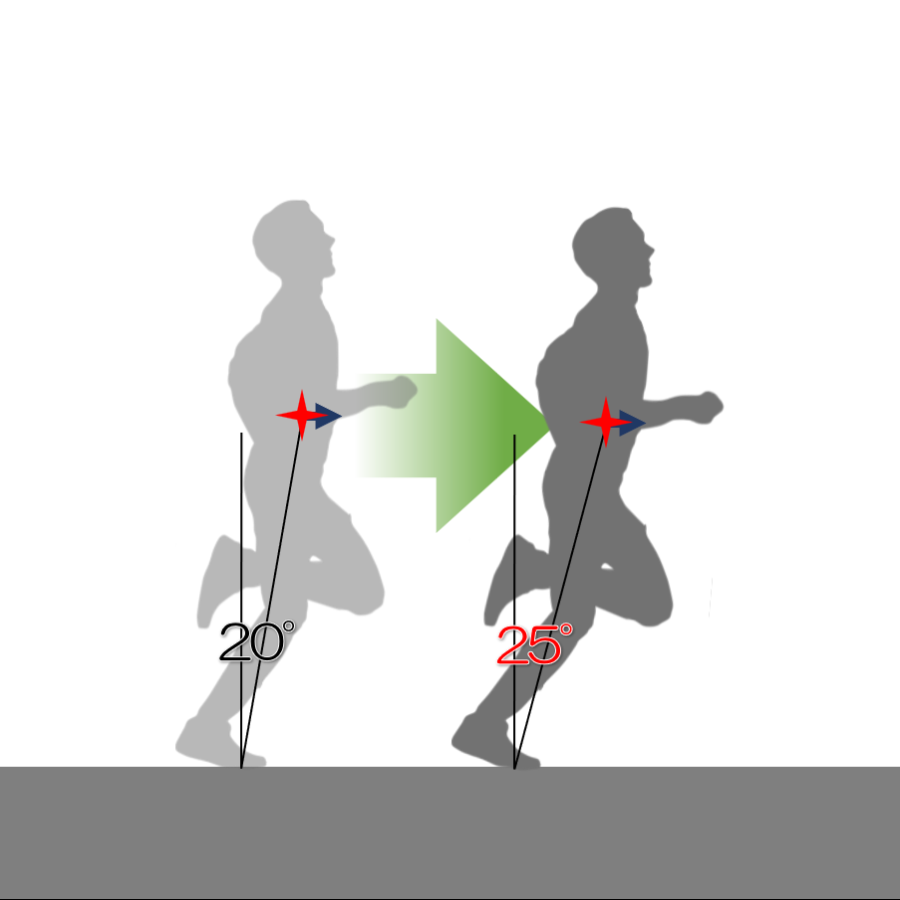
- 接地時間を長くする試みとして身体の傾きθの範囲を25°まで拡大した。
- 水平方向と垂直方向の筋力の仕事量を算出することでランニングエコノミーを可視化した。
- 傾きの範囲が拡大することで速度が増加し、効率も向上するが、その分だけ一歩で必要とされる仕事が増加した。
接地時間を長くするには、また、2つの方法があります。1つは、身体の傾きの範囲を大きくすることです。身体を20°まで倒した時点で離地するのではなく、もっと大きな角度まで接地を続けたら、その分だけ接地している時間が伸びます。滞空時間を0.2秒に固定したまま、身体の傾きθを25°まで倒した場合を算出してみました。1歩において身体の傾きは0°から20°の範囲で計算していたところ、22°と25°の範囲で計算しました。このとき、角度の分割数は20で一定です。つまり、22°のときは1.1°刻み、25°のときは1.25°刻みとしました。
ランニングエコノミーの可視化
滞空時間と接地時間の比率が変わることで、ランニングエコノミーが変化すると予想されます。そこで、今回は、ランニングにおいて発揮しなければならない筋力による仕事量を算出することで、ランニングエコノミーの可視化を目指しました。
筋力の作用により水平方向になされた仕事Whと垂直方向になされた仕事Wv集計しました。何故、2つを分けるかと言えば、後者は本質的に不要な仕事だからです。滞空時は重心が自由落下しますので、着地したときには重心の高さhが1mから減少します。すなわち、位置エネルギーを失います。この減少分を回復させるために、必ず、筋力を使います。これがWvです。ランニング中の上下動が激しいほど、Wvが大きくなります。ランニングに必要なのは、重心の水平方向の移動のみであり、重心の上下動は不要です。つまり、全体の仕事に対するWvの割合が小さいほど、無駄のないランニングであるということがわかります。
ただし、重力加速度が一定で、滞空時間が一定ならば、1回の滞空で失う位置エネルギーは一定となりますので、それを回復する仕事も一定になります。比較には100m地点での値を用いました。つまり、平衡速度に達した状態での比較ということです。
位置エネルギーの再利用
ランニングエコノミーを見積もる前に、位置エネルギーの再利用について考えておきたいと思います。
一部のランニング本では、高く跳躍して落下するエネルギーを推進力に変えればスピードが出ると言われています。地面に対して足を強く接地することで反発が得られるのだという主張でえす。一方で、足首を使って地面を後方に蹴ることは否定しているのです。接地の最後に蹴るのではなく、接地した瞬間に反発力を得るのだと言われると、正しそうに聞こえますね。しかし、本当にそうでしょうか。
接地した瞬間に発生する力の向きは理想的な状況でも垂直方向上向きです。垂直方向上向きの力を受けても、推進力にはなりません。現実には、着地の瞬間には垂直方向上向きよりもやや後ろ向きの力が発生しています。地面からの反発力をまともに受けたらブレーキがかかってしまいます。また、反発力をそのまま重心に作用させたら、身体が上方に移動してしまいますが、実際にはそうなってはいません。
人間の身体は弾性体なのか
着地によりアキレス腱に弾性エネルギーが蓄積するので、それを解放することで速度が上がる。人間の身体をボールのように弾ませる。などという記述も見られますが、人間の身体が弾性体と仮定するのは無理があります。
人間の身体が弾性率数十%の物体であるならば、高く跳躍するためには、予備の跳躍を繰り返せば良いでしょう。ちょうど、トランポリンの選手が演技を始める前の準備をするようなプロセスになります。トランポリンを支持するばねが蓄積する弾性エネルギーに対して、人間の筋力による跳躍が積み重ねることにより、高さ8mにも届く跳躍が可能になります。実際には、人間が垂直跳びを繰り返しても、跳躍の高さが高くなっていくことはありません。高く跳ぼうとする人は身を屈めて、1回の跳躍で筋力を発揮できる距離を稼ぎます。バレーボールでも、バスケットボールでも、陸上競技でも、そうです。
例えば、あなたが高いところから飛び降りて着地したとき、身体が跳ねてしまうことなどありますか。全身を筋肉で強張らせていたら、元の高さの50%まで弾みます。そんな人はいません。ランニング中の着地でさえ、身体を強張らせてしまったら、身体が壊れてしまいます。人間の身体の反発弾性率はほぼ0%と考えて良いでしょう。人間が着地した後に再び跳躍するのは、落下のエネルギーを全身で分散して身体の組織を守りながら着地し、その後、筋力を使って重心を加速するからです。反発弾性により落下時の運動エネルギーの向きを逆にしているわけではありません。
よって、重力ランニングにおいては、滞空中の重心の落下による位置エネルギーの損失は、純粋に損失(再利用不可)として計上することにしました。重心の位置エネルギーの変換には接地が必要であるということで、一貫しています。
身体の傾きθの影響
滞空時間:0.2 s走行距離:100 m
| 身体の傾きθ/° | 0-20 | 0-22 | 0-25 |
|---|---|---|---|
| 100mまでの歩数 | 85 | 80 | 72 |
| 経過時間t/s | 25.76 | 24.48 | 22.80 |
| ピッチ/[歩/min] | 210 | 207 | 202 |
| 速度V/[min/km] | 3:58 | 3:46 | 3:30 |
| 水平方向の仕事Wh/J | 5326 | 5963 | 6837 |
| 垂直方向の仕事Wv/J | 9681 | 9074 | 8183 |
| 仕事の合計/J | 15007 | 15037 | 15010 |
| Whの割合/% | 35.4 | 39.7 | 45.5 |
身体の傾きの範囲を大きくすることで、次の傾向が見られました。
ピッチは減少しましたが、その傾向はわずかでした。ピッチの減少を狙っていたので、私にとっては意外でした。しかし、これは当然のことです。身体の傾きが大きくなることで、平衡速度が上昇するため、接地時間の増加によるピッチの減少分を打ち消してしまうのです。身体の傾きが大きくなると速度が上がるのは現実のランニングとも一致します。ともあれピッチ減少の傾向になりましたので、ピッチの数字自体は現実的な範囲に収まりました。
100mを走行するために、水平方向に筋力がした仕事Whは大きくなりました。これは効率が悪くなったわけではなく、単に速く走ったためです。現に、100m到達時間は25.8sから22.8sに大幅に減少しています。速く走れば、その分だけ疲れるのは避けられないことでしょう。これも現実と一致しています。
一方で、一歩で得られる推進力が大きくなり、少ない歩数で100mに到達したために、垂直方向に筋力がした仕事Wvは歩数に比例して減少しました。Whの割合を見てみると、圧倒的に改善していると言えます。
ならば、誰しも身体を大きく傾ければ速く効率的に走れるという結論が導かれるのですが、それができないから、現実に苦労するわけです。
現実には簡単に速く走れない理由
その理由の1つは実に単純で、筋力が足りないからです。平衡速度における一歩当たりの仕事Wも算出してみると、0°から20°までの場合で178Jでした。0°から25°までの場合は210Jとなり、約18%増加しています。この仕事量を一歩でこなし続けることが速く走るということなのです。
もう1つ興味深い結果としては、筋力の仕事のうち、半分以上が垂直方向の仕事に使われているということです。端的に言えば、半分以上の仕事が無駄になっていることを示しています。重心の位置が下がるのは滞空をするからです。滞空時間を短くすることで、無駄な仕事を削減できることは間違いありません。
次は接地時間を長くするもう1つの方法、重心の高さを増加させる方法を調査してみます。



“身体の傾きを拡大するとどうなる?ランニングエコノミーの可視化の試み” に対して1件のコメントがあります。