脚の入れ替えにかかる仕事を物理モデルで分析
滞空時間を短くすることで、エネルギー効率が向上することが示されました。その代償として、ピッチが上昇することもわかりました。すると、直感的に、ピッチが高くなるときつくなる、とランナーなら誰しも思うことでしょう。この点は、物理モデルには全く含まれていませんでした。そこで、本記事ではそれを物理モデルに取り込むことを目指します。つまり、脚の入替により生じる仕事を物理モデルで表現します。
- 脚の水平方向の入れ替え動作による仕事W2を定量的に表現した。
- 滞空時間を短くするほど、W2が増加することが示された。
- W2の増加分を考慮しても、滞空時間の短い方が全体の仕事は小さかった。
モデル策定の方針
物理的に計算を可能にするため、単純化します。
離地している脚の上下動は考慮しない。
現実の走動作では離地すると、脚は持ち上がります。脚の重心も上方に移動するわけです。しかし、このことは考慮しません。
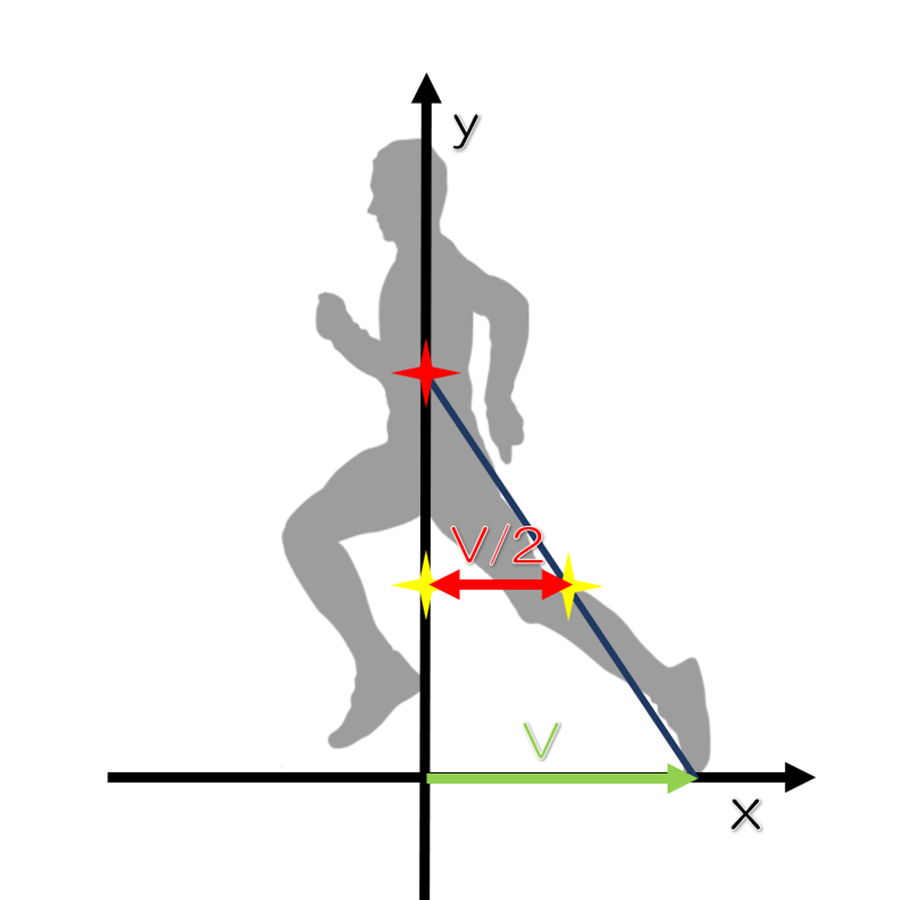
脚の移動の基準は重心とする。
脚を動かす仕事を計算するときに2つの基準が考えられます。1つは地面であり、もう1つは重心です。重心が地面に対して、単調に前方へ移動する一方で、脚は重心に対して前後に繰り返し移動します。このことから、本記事の課題に対しては、重心を基準として考えることにしました。水平方向の軸をx軸とし、重心を原点、後方を正、前方を負としました。
脚の重心は脚全体の中央に位置するものとする。
重力ランニングのモデルでは、身体の重心から地面との接点が脚ということになっています。脚が上から下まで質量が均等に分布しているのなら、中間点に重心があることになります。すなわち、地面との接地点と身体の重心の中間点に、脚の重心が位置するので、接地点の移動距離、移動速度の半分が、脚の重心の移動距離、移動速度になります。
脚の質量
脚の質量はどれくらいでしょう。私がインターネット上で調査したところ、身体全体の33%というものから20%よりも小さいという情報もありました。本記事では、切りの良い数字で片脚で10%、両脚で20%としました。つまり、脚1本は6㎏です。
脚の動き
走行中に、脚はどのように運動をしているのでしょうか。確定していることは、接地している脚の重心は、身体重心に対して、速度V/2で後方(x軸の正の方向)に動くということです。接地している間はこのルールに従います。離地したところから、別の動きを始めます。大きく分けて以下の4つの局面に分かれます。
- ステージ1. 離地した後、前方へ加速しているが、まだ、身体重心から見て後方へ移動している。
- ステージ2. 前方へ加速し続けた結果、身体重心から見て前方へ移動している。
- ステージ3. 身体重心から見て前方へ移動しているが、後方へ加速している。
- ステージ4. 後方へ加速し続けた結果、身体重心から見て後方へ移動している。
着地
着地するときには、身体の傾きθ=0°であるため、脚の重心も身体の重心の真下にあります。すなわち、x=0mとなります。また、そのときの脚の重心の速度は、走行速度Vの半分、すなわり、V/2です。
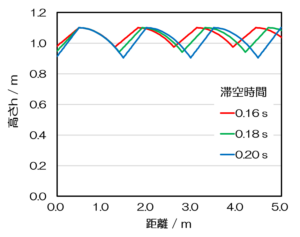
1サイクルの距離と時間
脚が離地してから着地するまでの過程を1サイクルと呼ぶことにします。脚は重心より後方の身体の傾きθ=25°の地点で離地します。その後、離地したところから重心の真下(θ=0°)まで戻ります。また、それに要する時間は、例えば、左脚なら、滞空時間(左脚が後ろ)+右足の接地時間+滞空時間(右脚が後ろ)で計算できます。
各滞空時間における条件は以下の通りです。
身体の傾きθの範囲:0°から25°重心の高さhの初期値:1.1 m
100 mにおける比較
体重:60㎏
片脚の質量:6㎏
*接地している間に身体の重心が進む距離
| 滞空時間/s | 0.20 | 0.18 | 0.16 |
|---|---|---|---|
| 速度V/[m/s] | 4.92 | 4.95 | 4.99 |
| 速度V/[分/km] | 03:23 | 03:22 | 03:20 |
| ストライド/m | 1.48 | 1.38 | 1.29 |
| ピッチ/[歩/min] | 200.0 | 214.8 | 232.2 |
| 接地距離*/m | 0.49 | 0.49 | 0.49 |
| 接地時間/s | 0.100 | 0.099 | 0.098 |
| 滞空距離/m | 0.99 | 0.89 | 0.80 |
| 1サイクルの時間/s | 0.50 | 0.48 | 0.46 |
仕事が最小となるように
これらの条件をおいて、脚の重心が水平方向の前後だけに繰り返し移動します。これを実現するために、筋力によって水平方向前後に任意の応力を発生させるわけです。「応力 × 時間 = 質量 × 速度の変化」の等式より、応力から速度の変化を導きだします。速度を時間で積分して、重心位置の変化を導き出します。このとき、どれだけの時間、どれだけの応力を発生させるかが問題となるわけですが、応力の和を最小二乗法で最小化することで決定しました。
以下のグラフは脚の重心の移動のサイクルです。滞空時間0.2 sの場合を例に取ります。x=0.24 mの地点で離地した後、0.35 mまで脚が後方(正の向き)に流れますが、ここから前方(負の向き)へ動き出します。その間、0.09 sです(ステージ1)。次に前方へ加速し、かつ、前方へ移動していきます(ステージ2)。しかし、0.25 s後、0.16 m地点では減速を開始します。後方へ加速しているということです(ステージ3)。そして、0.42 s後には、-0.08mの位置から後方へと移動し始めます(ステージ4)。そして、0.50 s後に重心の真下に着地します。
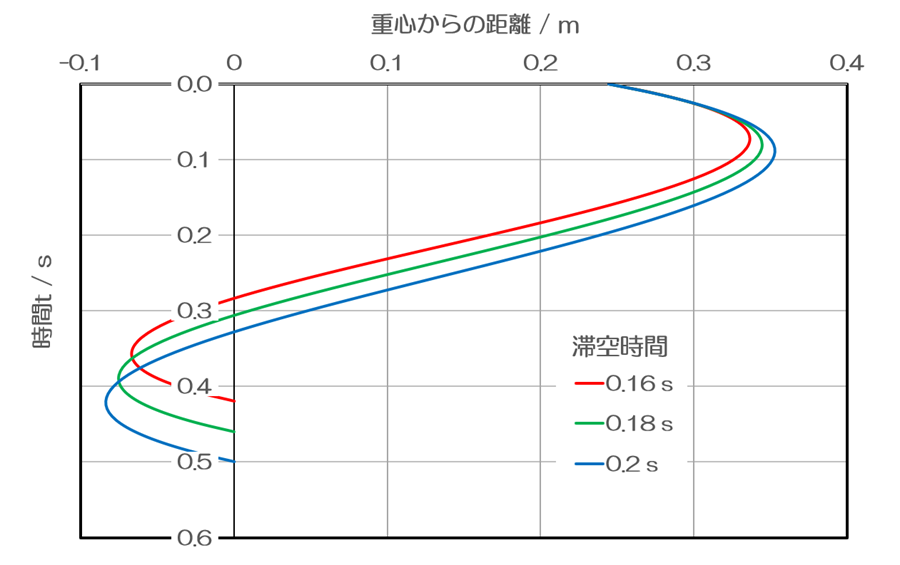
以下は脚の重心の速度をプロットしたものです。t=0 sにおいて走行速度の半分V/2から出発し、負の値(前方への速度)を取った後、V/2に戻ります。どれも放物線になっています。つまり、脚の重心に作用する力の変化は直線的であるということがわかります。
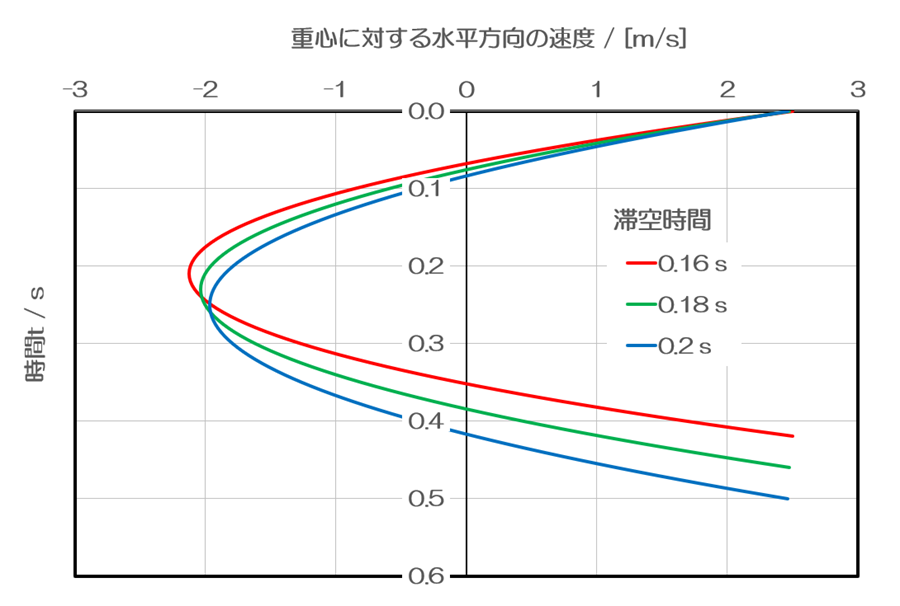
以下は脚の重心に作用する力をプロットしたものです。1サイクルの中で、負の値から正の値へと線形的に増加しています。
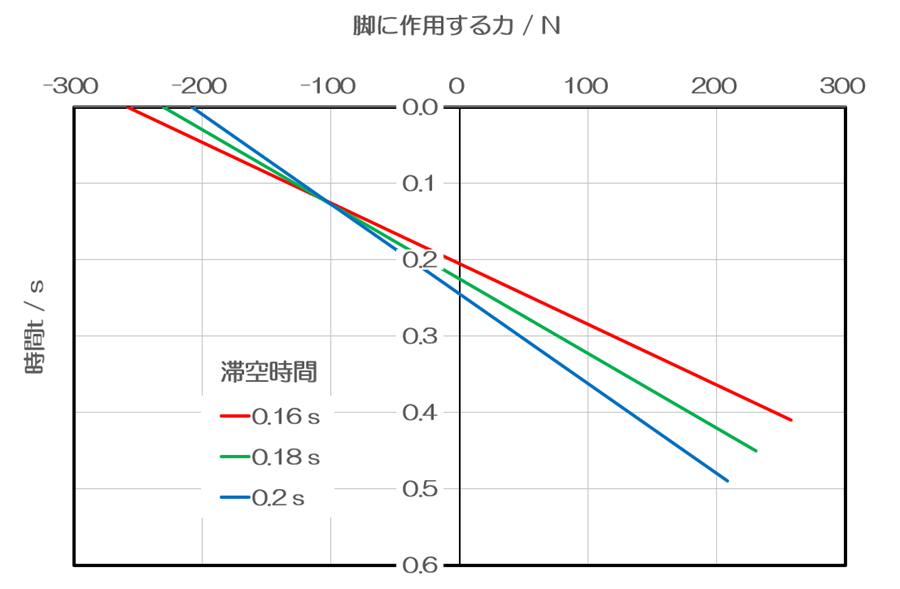
滞空時間の初期においては、前方へ最も強い力を発揮して脚を前方へ加速します。つまり、脚を後方から前方へ引き付けます。そこから徐々に力を弱めていき、中間点では力は0になります。サイクルの後半は徐々に脚を引き付ける力を強めていき、着地の直前に最も強い力で引き付けるのです。
このグラフから私はとても興味深いことを読み取りました。着地の瞬間に最も強い力で引き付ける、という点です。本記事で議論しているのは、水平方向だけの話です。着地点は身体の真下である以上、その直前には脚が重心の前方に位置しています。このため、引き付けなのです。そして、最も強く、というのも聞いたことがありません。
テレツ氏の指導では、身体の真下の地面を踏みつける、と表現されています。着地の瞬間に着目している点では同じですが、テレツ氏の言葉は、地面を垂直方向下方に筋力を発揮することを明らかに意味しています。このグラフから導かれる結論であるところの、水平方向後方に強く筋力を発揮するのとは、物理的に違うことを意味しています。もしかすると、テレツ氏の言葉から、垂直方向の踏みつけ動作のために、その直前の水平方向の引き付け動作が発生することはあるかも知れません。
脚の入れ替えの仕事
脚の質量に対して水平方向の前方および後方への加速を行うための仕事W2を計算してみました。この仕事は、身体の全体の質量を前方へ移動させる仕事Wとは別に発生します。
| 滞空時間/s | 0.2 | 0.18 | 0.16 |
|---|---|---|---|
| 脚の入替の仕事W2/[kJ/km] | 37.4 | 41.2 | 46.0 |
| 垂直方向の仕事Wv/[kJ/km] | 111.2 | 99.5 | 87.7 |
| 水平方向の仕事Wh/[kJ/km] | 102.8 | 107.7 | 114.2 |
| 合計の仕事W/[kJ/km] | 214.0 | 207.2 | 201.9 |
| 合計の仕事W+W2/[kJ/km] | 251.4 | 248.4 | 247.8 |
W2は滞空時間が小さくなると、大きくなります。1つには、脚をより短時間で加速するため、もう1つには1kmをカバーするのにより多くの歩数を必要とするためです。つまり、滞空時間を短くすると、脚の入れ替えにかかる仕事が増えるのです。
滞空時間0.2 sの場合、Wに対してW2は17%ですが、滞空時間0.16 sの場合、23%でした。この割合は、身体の質量に対する脚の質量%が増加するごとに、正比例で増加します。逆に言えば、脚の質量%が減少することで、正比例で減少します。改めて言われるまでもないことですが、脚が軽い方がピッチを高めても負荷が小さいのです。
このように、W2の増加が見られましたが、今回の設定条件では、合計の仕事W+W2は、依然として、滞空時間が0.16 sのときに最小でした。速度が大きく、仕事が小さいのであれば、何も問題はありません。滞空時間を短くするべき、という結論が維持されました。
やや複雑になってきましたが、脚の水平方向の入れ替えの仕事を定量的に評価することができましたので、次は脚の上下動を含めてみたいと思います。