入れ替え時の脚の上下動がランニングに与える影響を解明
水平方向の脚の入れ替えサイクルを表現することができました。しかし、人間の脚の入れ替えには脚の上下動が伴います。本記事では、この上下動を物理モデルで表現してみたいと思います。
- 脚の入れ替え動作の上下動のランニング全体の仕事における寄与は小さかった。
- 滞空時の身体の重心の落下を加味して、身体の重心に対する接地点の軌道を導いたところ、接地の直前に接地点を引き上げていた。
接地点の定義
これまで、脚の重心が水平方向に動くことだけを想定していました。当然ですが、脚を入れ替えるためには、離地しなければなりません。つまり、脚の接地点と地面の間に距離が生じます。そのためには、脚を持ち上げなければなりません。その結果、脚の重心が持ち上がります。前回の記事では、脚の重心は脚全体の中央に位置するとしただけですが、接地点についてもう少し定義しておかなければなりません。接地点とは、脚の中で地面と接地する面の中心として定義される概念上の点です。脚の接地点は身体の重心から見て、脚の重心の方向に2倍の距離にあります。
脚がどのような上下動をするか
エリートランナーの脚の動きを見ていると、調和が取れていて、無駄がありません。足の動きに注目すると、離地した後に複雑な軌道を描いて、着地するように見えます。しかし、物理層における議論では、現実の人間の足の動きを考えず、物理的にどのような動きが効率的であるかを考えます。
要は、接地点が地面を離れ、最高点まで上昇した後、地面に接するという単純な過程であるとみなします。そのような過程は無限に存在します。効率的な過程とはどのようなものでしょうか。
- 上昇と下降は単調な過程とします。つまり、上がるときは上がり続け、途中で少しだけ下がるようなことはありません。下がるときも同様です。
- 最高点まで1回、一瞬のみ到達することにします。最高点の高さは後で決定できるパラメータと考えます。
- 物理現象を考えるとき、物理的パラメータの変化に不連続点が生じない方が自然です。そこで、離地後に上昇を開始する瞬間、また、接地する瞬間に、高さの変化率がゼロであるようにします。
ここまで条件を付加しても、結局、軌道を1つに絞り込むことはできません。しかし、ランニングにおける接地点の動きは周期的な動きであることは確かですから、フーリエ展開で表すのに適しています。とは言っても、三角関数の複雑な級数を組み立て、人間の足の動きを表現するつもりはありませんので、安心してください。ただ簡単に、1つの三角関数で、接地点の上下動を表してみます。
脚が離地した瞬間は、高さの変化率が0で、直後から上昇していく必要があります。その後最高点に到達してから、同じ高さまで戻ってきて接地します。接地の瞬間はまた、高さの変化率が0になります。sinθでもcosθでもそのような関数を選ぶことはできますが、ここでは、わかりやすいように、sinθを-90°から270°までを使うことにします。
前の記事の水平方向の動きをx軸に割り当て、上記三角関数をy軸に割り当てます。θの変化は時間tに正比例とします。ということは、離地から接地までのちょうど半分の時間で最高点に到達します。
要は前の記事のグラフに、円周上のy座標の動きを割り付けただけです。その結果が以下の通りです。原点は身体重心です。脚の重心の動きを表していますので、脚の重心はy = -0.55mから出発し、y = -0.55mで1サイクルが終わります。最高点の高さは0.1mとしました。
最高点に対して、前方と後方が線対称です。巡航時には、まるで無限軌道のように脚の重心が動けば足りると思います。この軌道のことを、やわらかいお餅が自重でつぶれた形に見えることから、お餅型と呼ぶことにします。
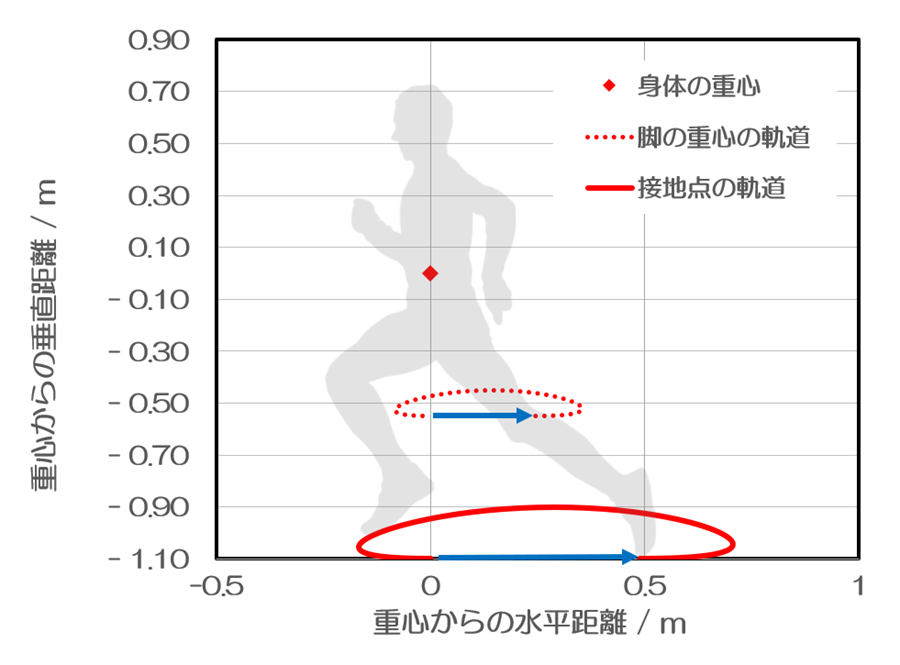
わかりやすく人間のシルエットを乗せてみると以下のような図になります。見易さのため、滞空時間0.2sの場合だけを表示します。上のグラフで示されていた脚の重心の動きは点線で表されています。そして、定義の通り、接地点は身体の重心に対して、脚の重心の倍のところにありますので、実線で示す通りの軌道を描くことになります。脚の重心が0.1m上昇するとき、接地点は0.2m上昇します。身体の重心を原点として、脚の重心が描くお餅型の軌道を2倍に拡大したものが接地点の軌道です。接地点と地面の間の距離は最高点において0.2mとなります。
滞空時の落下を考慮する
接地点がお餅型の軌道を描くと書きましたが、軌道を描く途中で、ランナーは2回の滞空を行います。滞空中は、両脚の支えを失いますので、身体の重心は否応なしに自由落下します。
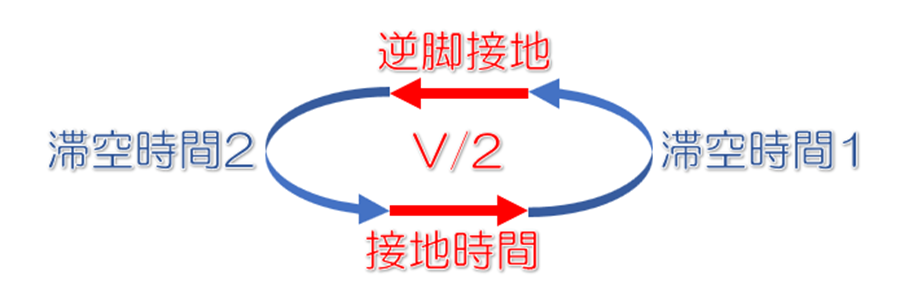
0.2sであれば、必ず、約20cm落下します。したがって、きれいなお餅型の軌道を描くことなどできずに歪んでしまいます。どの程度歪むのでしょうか。滞空中の自由落下を考慮したグラフを書いてみました。
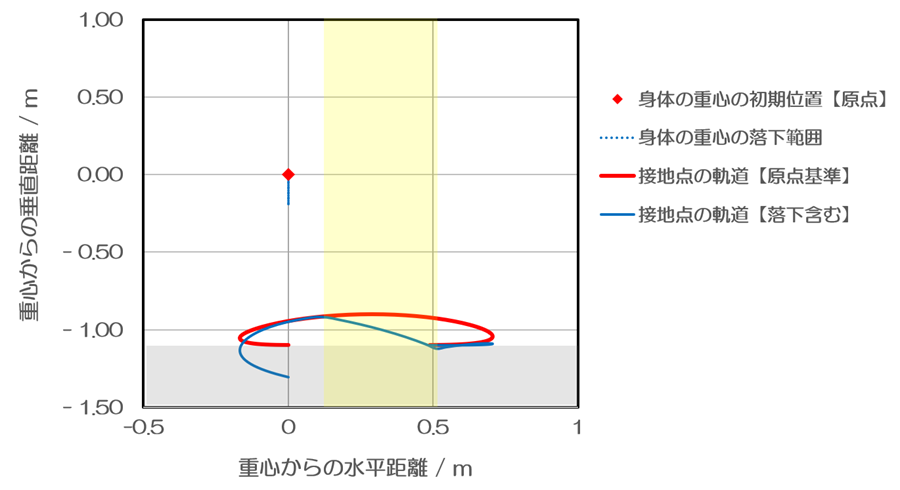
原点から下向きに伸びる青の点線が、滞空中の自由落下により、身体の重心が移動する落ち幅です。そして、青の実線が落下を考慮した後に接地点の軌道です。予想されたことですが、自由落下によって軌道は大きく変形しました。滞空時間1においては、地面のギリギリを這うように軌道が潰されてしまいました。これは、お餅型の軌道の最高点を少し高く変更すれば補填することができます。しかし、滞空時間2においては、問題はより深刻です。軌道が地面に深く入り込んでしまいました。x = -0.17 mのところでy = 0 mを通過しています。この点において、高さの変化率は0ではなく、大きいため、自由落下の加速度により、地面に激しく衝突するように着地することになっています。また、着地した地点が重心よりも前方ですから、ブレーキをかけてしまっています。重力加速度を敵に回してしまい、重力ランニングが崩壊したと言って良い状況です。
落下を相殺する
実際の人間は、滞空中の自由落下がある中でも、ランニングを成立させています。どのようにそれを実現しているのかと問われれば、ほとんどの人が跳躍によって実現しています。跳躍とは、ジャンプです。自由落下によって重心の高さが小さくなることを避けるために、予め上方に跳ぶのです。先に、重心の高さを稼いでおけば、その後、自由落下して高さを失っても、同じ重心の高さで接地することができます。いわば、先行投資です。
重力ランニングでは、離地するときに重心の高さを稼ごうとはせずに、そのまま水平方向に移動し続けます。したがって、自由落下により、すぐさま重心の高さを失います。それがゆえに、地面に衝突してしまうのです。では、どうしたら良いのでしょうか。実は簡単なことです。重心の高さを失った分だけ、脚を短くすれば良いのです。離地するときと着地するときで、脚の長さが同じである必要性はありません。
物理モデルであれば、脚を短くすることは可能だが、現実の世界では、人間の脚を短くすることなどできないと言う方がいるかも知れません。物理モデルにおける脚の長さとは、単に身体の重心から接地点の距離です。実際の人間であれば、身体の重心と足の裏です。脚を短くするとは、膝をより深く曲げた状態で脚を使うことを意味します。そもそも、人間が走っているとき、人間の膝は完全に伸長することはありません。多かれ少なかれ屈曲した状態のまま運用されています。また、誰もが知っていると通り、膝の関節の曲がり具合はランニング中、刻一刻と変化しています。つまり、脚の長さは常に変化しているのです。そうであれば、接地点の高さも、脚の長さの変化の範囲で変えられます。よって、接地点が地面に対してお餅型の軌道を描くためには、身体の重心の自由落下の分だけ、接地点を持ち上げてあげれば良いのです。
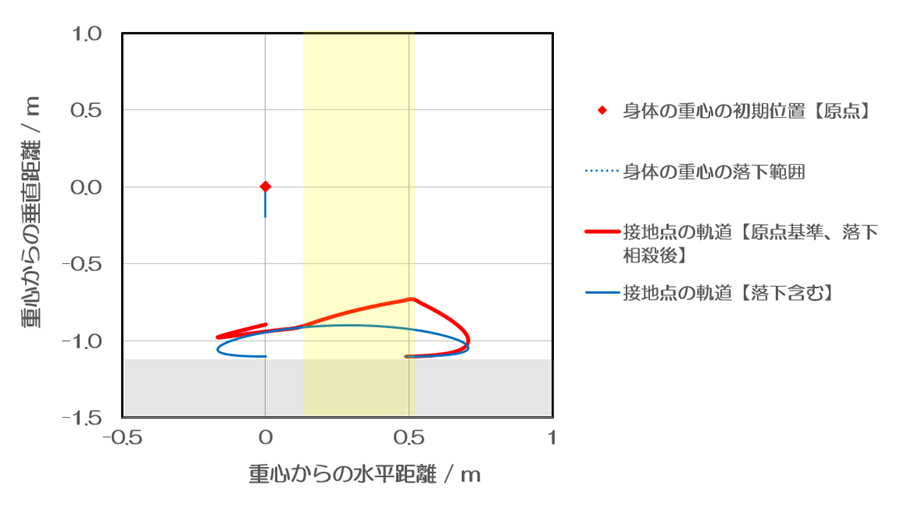
接地点が地面に対してお餅型の軌道(青線)を描くために、接地点を身体の重心に対してどのように動かすのか(赤線)を示したのが上のグラフです。離地した後に、身体の重心の自由落下が始まりますので、これを相殺するために、赤線が青線よりも徐々に上に離れていきます。身体の重心から見ると、落ち幅の分だけ接地点を持ち上げているわけです。離れ方は時間の二乗に比例しますので、後半ほど差が大きくなります。
赤線が折れ曲がっているところがありますが、ここから逆脚が接地しています。重心の高さが回復しますので、これにともない、赤線が青線に近づいていきます。赤線が青線と再び重なったところから、逆脚が離地します。つまり、また、身体の重心の自由落下が始まります。一方で、接地点を地面に向けて降ろしていく局面でもあります。ここで、自由落下を相殺するように接地点を持ち上げると、赤線は最前点(x = -0.17 m)に到達した後に、上昇しながら(y軸正の向き)、x = 0 mに近づいていきます。
私はこれに驚きました。接地の瞬間には、足を引き戻しつつ(x軸正の向き)、持ち上げる(y軸正の向き)のが正解という指摘です。自分自身が走っているときに、足を引き戻している意識はありましたが、足を降ろしていると思っていました。地面に対しては間違いなく降ろしているのですが、身体の重心に対しては持ち上げていると思っていませんでした。しかし、こうしてグラフで示されれば、この指摘は事実です。突き詰めて考えればわかることなのです。私自身が走っているときに、地面基準の動きと身体の重心基準の動きを区別していない、あるいは、混同していることを知らされました。身体が自由落下しているのに、足を身体の重心に対して持ち上げないでいたら、地面に激しく衝突してしまいます。ですから、無意識ではありますが、身体の重心に対して足を持ち上げながら接地して、身体を保護していると考えます。
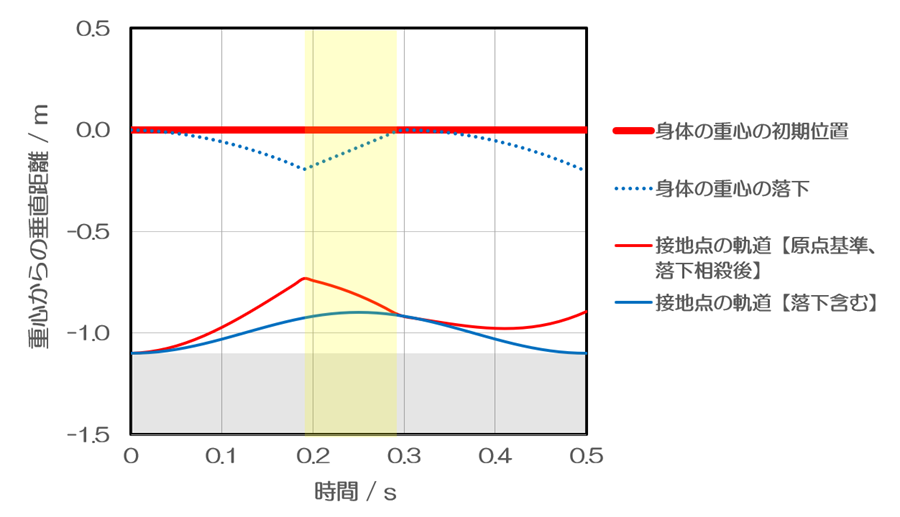
上のグラフでは横軸に時間を取り、縦軸に重心と接地点の高さを取りました。青い線を見てみると地面基準において、身体の重心と接地点の動きがわかります。身体の重心が上昇と落下を繰り返す一方で、接地点は滑らかな上下動を示します。赤い線を見てみると、身体の重心基準の接地点の移動がわかります。
滞空時間の影響
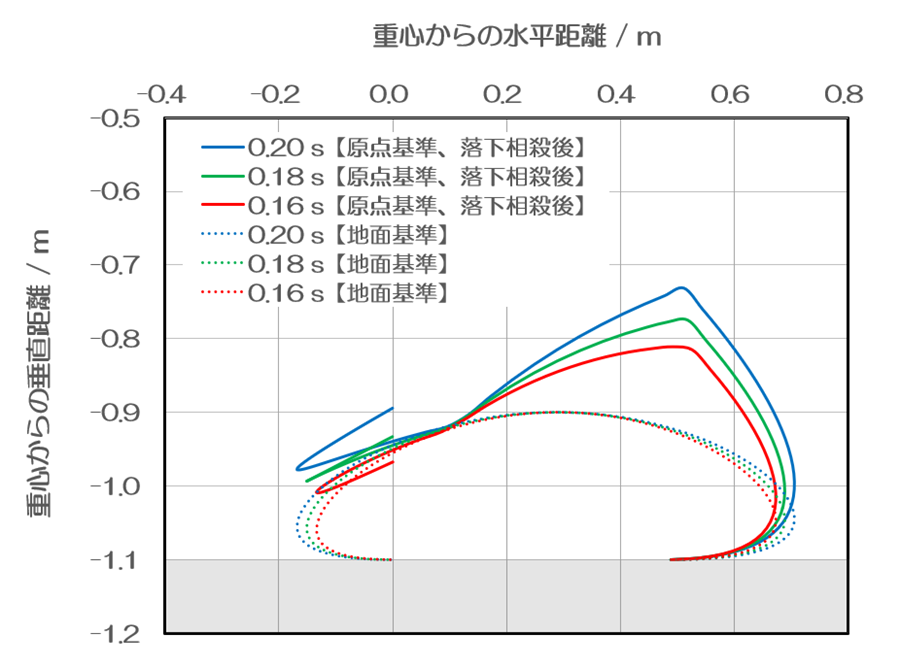
滞空時間により、接地点の移動がどのように動くかを比較してみましょう。滞空時間が長くなるほどに落ち幅が大きくなります。したがって、地面基準のお餅型の軌道に対して、原点基準の軌道がより大きく上昇します。接地点は地面に対して0.2mしか上昇しませんが、滞空時間が0.2 sの場合、約0.37m上昇します。それでも、身長は190cmという想定ですから、現実的な数字です。接地点を持ち上げると言っていますが、地面に対してのお餅型の軌道が重力場に対する移動ですから、仕事の算出において、こちらだけを考慮すれば良いことになります。
身体の傾きθの範囲:0°から25°重心の高さhの初期値:1.1 m
100 mにおける比較
体重:60㎏
片脚の質量:6㎏
*接地している間に身体の重心が進む距離
| 滞空時間/s | 0.20 | 0.18 | 0.16 |
|---|---|---|---|
| 速度V/[m/s] | 4.92 | 4.95 | 4.99 |
| 速度V/[分/km] | 03:23 | 03:22 | 03:20 |
| ストライド/m | 1.48 | 1.38 | 1.29 |
| ピッチ/[歩/min] | 200.0 | 214.8 | 232.2 |
| 接地距離*/m | 0.49 | 0.49 | 0.49 |
| 接地時間/s | 0.100 | 0.099 | 0.098 |
| 滞空距離/m | 0.99 | 0.89 | 0.80 |
| 1サイクルの時間/s | 0.50 | 0.48 | 0.46 |
| 滞空時間/s | 0.20 | 0.18 | 0.16 |
|---|---|---|---|
| 脚の入替の仕事W2v/[kJ/km] | 4.0 | 4.3 | 4.6 |
| 脚の入替の仕事W2h/[kJ/km] | 37.4 | 41.2 | 46.0 |
| 脚の入替の仕事W2/[kJ/km] | 41.4 | 45.5 | 50.5 |
| 垂直方向の仕事Wv/[kJ/km] | 111.2 | 99.5 | 87.7 |
| 水平方向の仕事Wh/[kJ/km] | 102.8 | 107.7 | 114.2 |
| 身体の重心移動の仕事W/[kJ/km] | 214.0 | 207.2 | 201.9 |
| 合計の仕事W+W2/[kJ/km] | 255.4 | 252.7 | 252.4 |
脚の入れ替えの仕事W2を水平方向の成分W2hと垂直方向の成分W2vに分けました。本記事で新たに加わるのはW2vです。脚の重心の位置エネルギーの獲得量を一歩ごとに計算し、1km当たりの仕事を算出しました。脚の降下による位置エネルギーの損失は回収不能としています。と言っても、脚の重心の上下動は0.1mと決まっていますから計算は簡単です。W2vの寄与は合計の仕事に対して、1.5~1.8%となりました。その結果、滞空時間による仕事の関係は覆りませんでした。つまり、滞空時間が短いほど、スピードが大きいし、仕事も小さいということです。ただし、脚の入替の仕事は滞空時間が短いほど大きくなります。
実は今まで、身体の傾きθを大きくしていくときに、前進するに従い、重心と接地点の距離が大きくなっていくことを無視していました。つまり、接地している間に脚の長さが伸びなければならず、脚の長さには上限があります。次はこの制約に関して考察します。


