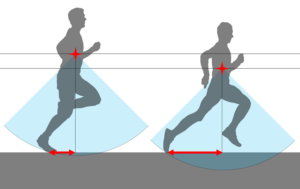
着地の仕事を含めてませんでした。重力ランニングの再評価
ここまで、重力ランニングのモデル化を進めてきました。脚の入れ替えを含めて、ランニングエコノミーを数値化できました。考え方が出来上がってきたので、シミュレーションの精度を高めようとしました。その中で1つ大きな間違いがあることに気が付きました。しかし、安心してください。大きな間違いではありますが、その間違いを修正することで、重力ランニングの正しさがより明確になるものです。
- 着地の仕事を含めることで、垂直方向の仕事の割合が増加し、水平方向の仕事の割合が減少した。
- 滞空時間の短縮によるエネルギー効率の改善が強調される結果となった。
着地の仕事
「身体の傾きを拡大するとどうなる?ランニングエコノミーの可視化の試み」において、ランニングエコノミーの可視化を行いました。このとき、位置エネルギーの再利用について考察しました。結論としては、位置エネルギーの再利用は不可です。つまり、身体の重心の自由落下により生じる垂直方向下向きの運動エネルギーは、ゴムボールがバウンドするように垂直方向上向きの運動エネルギーに変換することはできない、と書きました。この文は正しいのですが、モデル上の処理が問題です。
単に再利用は不可とみなしただけなので、身体の重心の落下により発生する運動エネルギーを消えてなくなったものとしていました。すなわち、ランニング中の垂直方向の仕事Wvに含めていませんでした。
しかし、身体の重心が自由落下により垂直方向下向きに加速した結果、脚を使って地面に着地するとき、脚は仕事をしている気がします。いや、むしろ、着地の瞬間は脚の筋力を明らかに使っています。これは、垂直方向下向きに加速した身体の重心を、地面に対して速度ゼロまで減速するという仕事をしているのです。もし、そうでないならば、延々と垂直方向下向きに自由落下するのが物理的に正しい結論です。
したがって、着地時の仕事を含めて、再計算したのが以下の内容です。
身体の傾きを拡大するとどうなる?ランニングエコノミーの可視化の試み
まず、「身体の傾きを拡大するとどうなる?ランニングエコノミーの可視化の試み」の計算結果は以下のように変更となります。着地時の仕事をWvに含めると、Wvがほぼ2倍になります。従来は、重心を持ち上げる仕事だけを考慮していましたが、持ち上げた分の位置エネルギーを着地時に相殺する仕事を含めたので当然の帰結です。
滞空時間:0.2 s走行距離:100 m
| 身体の傾きθ/° | 0-20 | 0-22 | 0-25 |
|---|---|---|---|
| 100mまでの歩数 | 85 | 80 | 72 |
| 経過時間t/s | 25.76 | 24.48 | 22.80 |
| ピッチ/[歩/min] | 210 | 207 | 202 |
| 速度V/[min/km] | 3:58 | 3:46 | 3:30 |
| 水平方向の仕事Wh/J | 5326 | 5963 | 6837 |
| 垂直方向の仕事Wv/J | 19445 | 18178 | 16459 |
| 仕事の合計W/J | 24771 | 24141 | 23296 |
| Whの割合/% | 21.5 | 24.7 | 29.3 |
その他の部分は同じです。Wvが2倍になることは、大きな違いをもたらします。Whの割合が、大幅に低下します。0-20°の場合、Whの割合は21.5%となります。修正前でもWhの割合が小さいと思っていたのですが、約8割が前進に関わりない仕事という驚きの結果になります。0-25°の場合には、Whの割合が29.3%となり、大幅な改善になります。
脚が長くなったら速く走れる?重心の高さとランニングの関係
身体の傾きθの範囲:0°から25°滞空時間:0.2 s
| 重心の高さh/m | 1.00 | 1.05 | 1.10 |
|---|---|---|---|
| 走行距離l/m | 100 | 100 | 100 |
| 歩数 | 72 | 71 | 69 |
| 経過時間t/s | 22.8 | 22.7 | 22.5 |
| ピッチ/[歩/min] | 202 | 199 | 197 |
| 速度V/[min/km] | 3:30 | 3:29 | 3:27 |
| 水平方向の仕事Wh/J | 6837 | 6980 | 7014 |
| 垂直方向の仕事Wv/J | 16459 | 16136 | 15778 |
| 合計の仕事W/J | 23296 | 23116 | 22792 |
| Whの割合/% | 29.3 | 30.2 | 30.8 |
次に「脚が長くなったら速く走れる?重心の高さとランニングの関係」です。こちらも同様の変化です。Whの割合は大きく下がって、3割程度となります。重心の高さによって、大きな変化はないという結論は変わりませんでした。
遂に滞空時間を短縮!長距離走における効率が改善
身体の傾きθの範囲:0°から25°重心の高さhの初期値:1.1 m
走行距離:100 m
| 滞空時間/s | 0.2 | 0.18 | 0.16 |
|---|---|---|---|
| 歩数 | 69 | 74 | 79 |
| 経過時間t/s | 22.5 | 22.4 | 22.3 |
| ピッチ/[歩/min] | 197 | 211 | 228 |
| 速度V/[min/km] | 3:27 | 3:26 | 3:24 |
| 水平方向の仕事Wh/J | 7014 | 7133 | 7242 |
| 垂直方向の仕事Wv/J | 15778 | 13633 | 11511 |
| 合計の仕事W/J | 22792 | 20766 | 18753 |
| Whの割合/% | 30.8 | 34.3 | 38.6 |
「遂に滞空時間を短縮!長距離走における効率が改善」の計算結果も修正しました。やはり、Whの割合が小さくなりました。滞空時間が0.20 sから0.16 sにされたとき、修正前は47.2%から55.7%で、18%の改善でした。しかし、修正後は、30.8%から38.6%となり、25%の改善です。つまり、滞空時間を短縮することによる効率の改善幅が大きくなりましたので、重力ランニングの正しさがより強調された格好です。
脚の入れ替えにかかる仕事を物理モデルで分析
身体の傾きθの範囲:0°から25°重心の高さhの初期値:1.1 m
100 mにおける比較
体重:60㎏
片脚の質量:6㎏
| 滞空時間/s | 0.2 | 0.18 | 0.16 |
|---|---|---|---|
| 脚の入替の仕事W2/[kJ/km] | 37.4 | 41.2 | 46.0 |
| 垂直方向の仕事Wv/[kJ/km] | 233.2 | 208.8 | 184.2 |
| 水平方向の仕事Wh/[kJ/km] | 102.8 | 107.7 | 114.2 |
| 合計の仕事W/[kJ/km] | 336.1 | 316.5 | 298.2 |
| 合計の仕事W+W2/[kJ/km] | 373.5 | 357.7 | 344.1 |
「脚の入れ替えにかかる仕事を物理モデルで分析」における「脚の入れ替えの仕事」の計算結果です。修正前は、合計の仕事W+W2の値が、滞空時間によってほぼ変わらないレベルまで近づいていました。しかし、修正後は、滞空時間が短くなることで、W+W2が依然として8%減少することになりました。Wvが大きくなったため、脚の入替の仕事W2を考慮した後でも、滞空時間が短い方が、エネルギー効率の優位性が維持されています。
入れ替え時の脚の上下動がランニングに与える影響を解明
| 滞空時間/s | 0.20 | 0.18 | 0.16 |
|---|---|---|---|
| 脚の入替の仕事W2v/[kJ/km] | 4.0 | 4.3 | 4.6 |
| 脚の入替の仕事W2h/[kJ/km] | 37.4 | 41.2 | 46.0 |
| 脚の入替の仕事W2/[kJ/km] | 41.4 | 45.5 | 50.5 |
| 垂直方向の仕事Wv/[kJ/km] | 233.2 | 208.8 | 184.0 |
| 水平方向の仕事Wh/[kJ/km] | 102.8 | 107.7 | 114.2 |
| 身体の重心移動の仕事W/[kJ/km] | 336.1 | 316.5 | 298.2 |
| 合計の仕事W+W2/[kJ/km] | 377.5 | 361.9 | 348.7 |
最後に、「入れ替え時の脚の上下動がランニングに与える影響を解明」の修正です。こちらは、脚の入替の仕事W2vの寄与が小さいという結論は変わりませんでした。