重心の高さで速度が変わる?ストライドとピッチの関係を明らかに
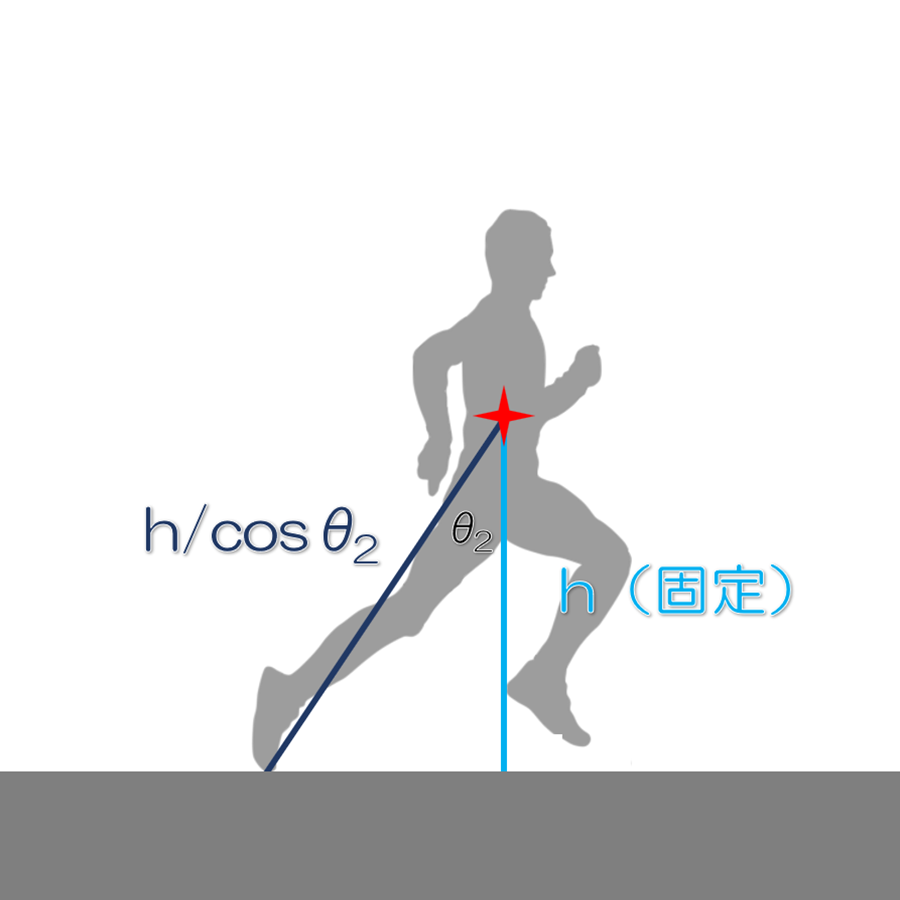
従来hは重心の高さの初期状態としていました。それは、自然に考えると人間の立位における人間の身体の重心の高さということになります。つまり、脚を伸ばした状態と想定していました。しかし、上の図に示すように、実際には、離地する寸前にh/cosθまで伸長しなければなりません。cosθは1以下ですから、h/cosθはhよりも大きい値です。つまり、hは既に脚を伸ばした状態であったはずなのに、離地するまでの動作でさらに伸ばすことになっていました。ただ、このことには、現実に照らして矛盾はありません。人間の脚が離地する瞬間はつま先が残るからです。おおよそ踝からつま先までの長さは追加で伸びる余地があります。
- 離地した瞬間の接地点と身体の重心の距離Hを固定値とした。
- 離地した瞬間の身体の傾きθ2を大きくしていくほど、速度が増加した。このとき、ストライドが拡大し、ピッチが減少した。
- 身体の重心の高さhは、θ2を大きくするほど低下した。したがって、速度が増加するほど、身体の重心の高さhは低下することが示された。
重心の高さに関する考察
脚が伸びる余地があったのは確かですが、限界があります。つまり、離地する瞬間の接地点と身体の重心の距離が実際のランニングにおける制約事項なのです。これは、おおよそつま先立ちしたときの身体の重心の高さと一致すると考えます。
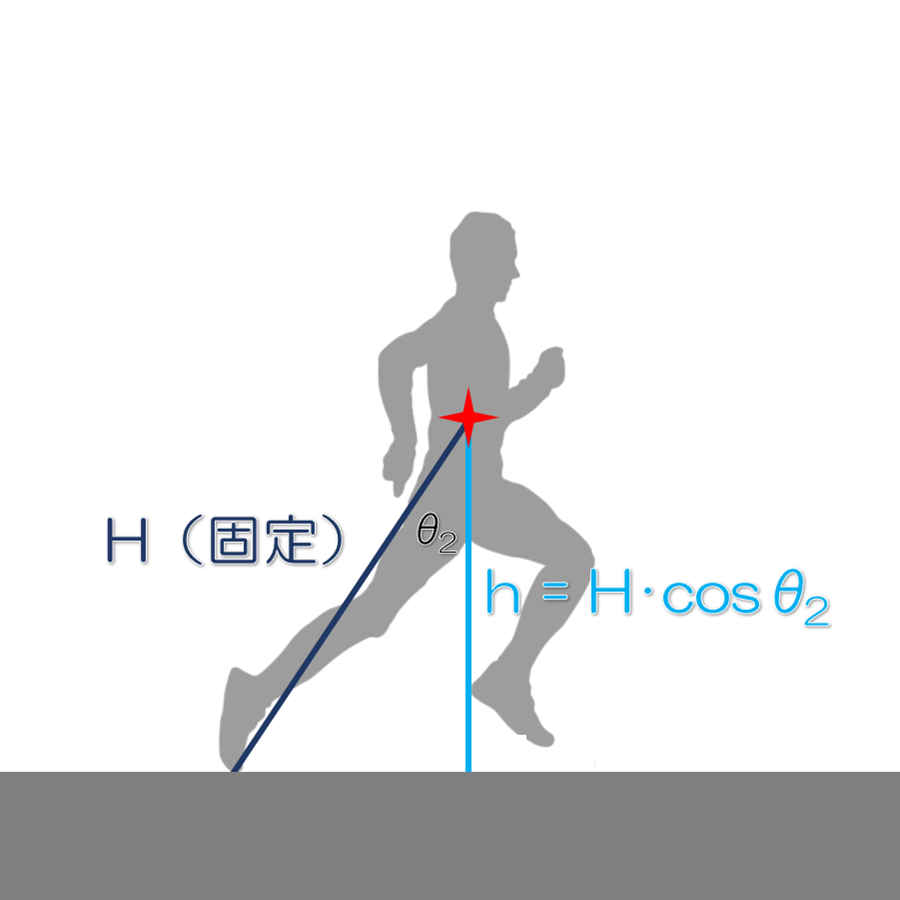
今までは伸長190cmで重心の高さh=1.1mと設定して、固定していました。今回は、垂直の辺hではなく、斜辺のHを固定してシミュレーションを行いました。すると、hは立位における身体の重心の高さではなく、ランニング時における身体の重心の高さを意味することになり、身体の傾きθに従って変化します。このとき、h=H・cosθとなります。そして、H=1.1mとしました。
ここで、離地する瞬間の身体の傾きθ2におけるhの値をh2とします。従来は、hを固定していたため、θ2が変化してもh2が変わらず、Hが変化するという状態でした。Hが制約事項になっていないということは、離地時に脚を限界の長さまで使っていないということです。実際、θ2は25°という浅い角度を想定していました。これは到底、本気で走っているとは言えません。そこで、離地する瞬間に脚の長さを限界のHまで使ったうえで、離地時の身体の傾きθ2を変えていき、速度を調整する状態、つまり、本気のランニングに移行した訳です。
| θ2 | H・cosθ |
|---|---|
| 15 | 1.063 |
| 20 | 1.034 |
| 25 | 0.997 |
| 30 | 0.953 |
| 35 | 0.901 |
θ2を大きくしていくと、速度が増加するはずですが、同時にh2が小さくなっていくことがわかります。離地した瞬間の高さh2が小さくなるわけですから、そこから、自由落下が起こると、着地時にはさらに重心の高さが低下します。つまり、着地時の脚の屈曲が大きくなるということです。
着地時に脚が屈曲状態であると聞くと、余計な筋力が必要であるかのように感じられるかも知れません。もし、筋肉走りのように、高くジャンプする走り方であれば、その通りです。ジャンプした分の高さを相殺する筋力を発揮しなければなりません。
しかし、重力ランニングでは、滞空中にも身体の重心を上方に持ち上げることはありません。ただ自由落下させるだけです。とは言え、重力加速度によって、重心が垂直方向下向きに加速することは確かですから、滞空時間は短い方がベターです。しかし、このことは重力ランニングにおいて有利だと、今までも記載していた事項です。接地しているときに重心に作用する重力を変換して加速するのです。一方で、滞空中は加速することはできず、ただ空気抵抗によって減速するのみです。
それでは、エリートランナーレベルの1キロ3分で走ることを目指して、θ2を大きくした場合に、速度と重心の高さがどうなるかを見てみましょう。
シミュレーションの改善
ところで、今回からシミュレーションの方法を改良しました。
- 改善1:接地区間と滞空区間をそれぞれ20分割して計算していたところ、それぞれ50分割にしました。これは計算の精度を高めるためです。
- 改善2:上記を検討する中で、接地区間の0°からの動き出しの部分においては、分割を細かくしても誤差を生むことがわかりました。そこで、θ1は1°とすることにしました。
- 改善3:脚の切り替えの上下動における、脚を地面に接地するときの仕事を計算値に含めました。
したがって、今後のシミュレーションの方がより現実に近いことになります。
θ2を大きくしていく
まず、滞空時間を0.2 sとして、離地する瞬間の身体の傾きθ2を大きくしてみましょう。従来、θ2は25°までにしていました。それは、上記の議論をしていなかったため、傾きθ2を大きくしていくと誤差が大きくなるためでした。しかし、本記事では、Hを固定としていますので、θ2を大きくしていくと、hはこれを反映して、小さくなります。0.2 sのときは、さらに約20cmの滞空中の落下が加わります。θ2 = 35°の場合は、hは約70 cmから約90 cmの間で運用することになります。
滞空時間0.20 sの場合
滞空時間:0.20 s離地時の重心と接地点距離H:1.1 m
100 mにおける比較
体重:60 ㎏
片脚の質量:6 ㎏
| 離地時の身体の傾きθ2/° | 15 | 20 | 25 | 30 | 35 |
|---|---|---|---|---|---|
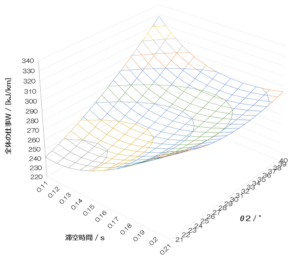
| 重心の移動の仕事W1/[kJ/km] | 289 | 249 | 228 | 218 | 216 |
| 脚の入替の仕事W2/[kJ/km] | 46 | 51 | 56 | 61 | 67 |
| 合計の仕事W/[kJ/km] | 336 | 300 | 284 | 280 | 283 |
| ストライド/m | 0.88 | 1.09 | 1.29 | 1.49 | 1.68 |
| ピッチ/[歩/min] | 208 | 201 | 196 | 192 | 189 |
| 速度/[min/km] | 5:29 | 4:34 | 3:57 | 3:30 | 3:09 |
| 身体の重心の高さの最小値hmin/m | 0.87 | 0.84 | 0.80 | 0.76 | 0.71 |
| 身体の重心の高さの最大値hmax/m | 1.06 | 1.03 | 1.00 | 0.95 | 0.90 |
これまで「重心の移動の仕事」をWと表記していましたが、ここからはこれをW1と表記します。そして、「重心の移動の仕事W1」と「脚の入替の仕事W2」の和を「合計の仕事W」と表記しました。間違いないように留意願います。
θ2が大きくなるに従い、ストライドが拡大し、ピッチが減少します。離地する瞬間の身体の傾きθ2が大きいということは、その分だけ脚を接地している距離が長くなります。したがって、ストライドも拡大します。逆に、ストライドが拡大すると脚の入替にかかる時間は大きくなるので、ピッチは減少します。
ストライドが拡大し、ピッチは減少しますが、速度は増加しています。このことから、速度増加の結果として、両方が互いに変化することがわかります。
興味深いことに仕事Wは、30°までは減少し、35°で増加に転じました。つまり、滞空時間0.2 sにおいてはθ2 = 30°が最も効率の良い点ということです。現実の世界において、速度と滞空時間のバランスが取れている、ということです。25°以下ではストライドが小さい割に滞空が長いし、逆に30°以上ではストライドが大きい割に滞空が短いのです。
また、θ2を35°まで大きくしてみましたが、1キロ3分に届きませんでした。
滞空時間の短縮の影響
では、滞空時間を0.16sとしたらどうなるでしょうか。まず、簡単に予想できることですが、ピッチが大幅に増加します。ただし、仕事Wは低下します。脚の入替で仕事が増加していますが、滞空が短くなることで身体の重心の上下動が小さくなるため、仕事全体としては現象するのです。仕事の極小値は、θ2=25°のときとなりました。滞空時間が短くなりましたので、よりストライドが小さいときにバランスが取れているということです。それでも、θ2=35°のときに、1キロ3分を下回ることができました。このとき、ピッチは221歩/minであり、非現実的ではありません。
滞空時間0.16sの場合
滞空時間:0.16 s離地時の重心と接地点距離H:1.1 m
100 mにおける比較
体重:60 ㎏
片脚の質量:6 ㎏
| 離地時の身体の傾きθ2/° | 15 | 20 | 25 | 30 | 35 |
|---|---|---|---|---|---|
| 重心の移動の仕事W1/[kJ/km] | 218 | 193 | 183 | 181 | 185 |
| 脚の入替の仕事W2/[kJ/km] | 60 | 67 | 74 | 81 | 88 |
| 合計の仕事W/[kJ/km] | 278 | 259 | 256 | 262 | 274 |
| ストライド/m | 0.78 | 0.98 | 1.16 | 1.34 | 1.51 |
| ピッチ/[歩/min] | 247 | 237 | 230 | 225 | 221 |
| 速度/[min/km] | 5:11 | 4:19 | 3:44 | 3:19 | 2:59 |
| 身体の重心の高さの最小値hmin/m | 0.94 | 0.91 | 0.87 | 0.83 | 0.78 |
| 身体の重心の高さの最大値hmax/m | 1.06 | 1.03 | 1.00 | 0.95 | 0.90 |
このように、1キロ3分のように高速で走るときには、θ2をある程度以上、大きくしなければなりません。このとき、滞空時間を短くすると速度が上昇し、仕事が減少する傾向が見られました。ただし、滞空時間をゼロにしたときには、ピッチが異常に大きな値となり、実現不可能となることは既にわかっています。次の記事では、滞空時間およびθ2と仕事Wの最適値を探すことにします。
腰の高さはどうあるべきか
ランニング中の腰は、高く維持するべきと多くのランニング本に書いてあります。
「胸を張る」、「腰を高く保つ」、「接地時間を短くする」が正しいランニングフォームを定義する要件のように喧伝されています。しかし、これは物理的には変です。
腰を高く保つのであれば、身体は立位に近くなりますので、以下の図で示すように接地している距離と時間は短くなります。その意味で、腰を高く保つことは、接地時間を短くすることに密接に関連します。ただ、これで速く走ろうとすると、物理的には明らかに困難が生じます。短い接地時間の間に、空気抵抗に打ち勝ち、加速するだけの運動量を身体の重心に与えなければなりません。つまり、短時間で地面に強い力を加え、反作用を得るのです。これは「地面を強く蹴る」という動作です。
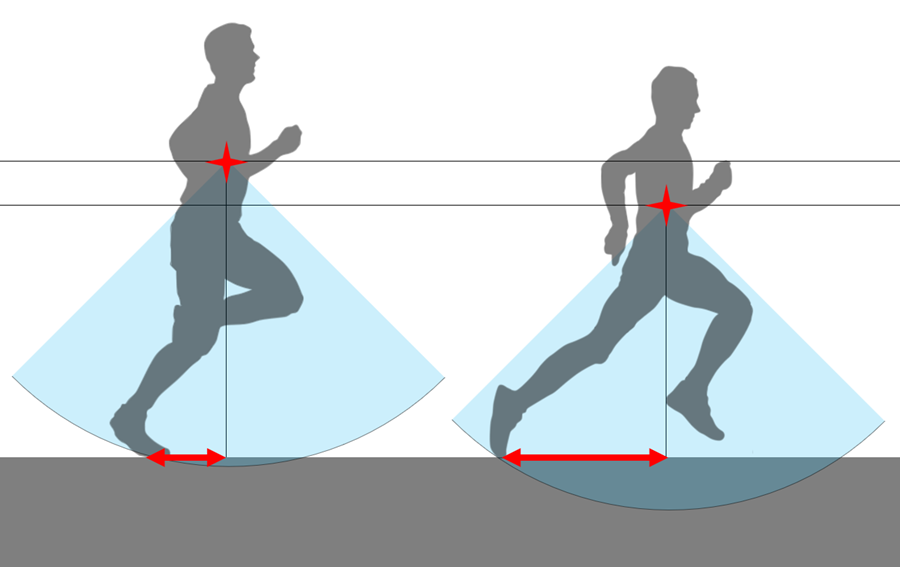
「腰を高く保つ」、「接地時間を短くする」、「地面を強く蹴る」は、ある種の走り方に関する一貫性のある記述なのです。ですから、地面を強く蹴らないが、腰を高く保つ、ということはできません。この走り方を私は「筋肉走り」と呼んでいます。
重力ランニングでは、既に述べたように、速度を増加させようとすると、腰の高さが低下するという物理的な結論を是とします。したがって、接地時間はできるだけ長くし、地面を全く蹴りません。これらは、重力ランニングに関する一貫性のある記述になります。
筋肉走りは、身体に負担がかかるため、強度を高めていくと早晩、故障に見舞われます。したがって、筋肉走りの指導・普及は適切に防止しなければなりません。また、世の中には、筋肉走りを否定しながら、実際には筋肉走りの本質を理解していないため、矛盾した記述をしているランニング本も多くあります。筋肉走りを正しく完全に否定し、重力ランニングを推奨するのが本ブログの趣旨であることは言うまでもありません。