遂に到達！速度と仕事の関係から導く、ランニングの最大効率

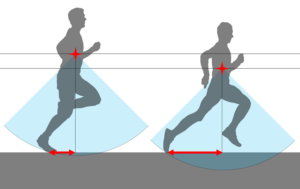
前の記事では、離地の瞬間の身体の傾きθ₂を大きくしていくことで、速度Vが増加し、ストライドが拡大し、ピッチが減少することがわかりました。また、滞空時間を0.20sから0.16sへ短縮することで、ランニングの全体の仕事Wが減少することがわかりました。一方で、θ₂を大きくしていく過程で全体の仕事Wが極小値を取ることもわかりました。

これらを箇条書きにまとめると以下のようになります。

θ₂を大きくする×滞空時間一定だと、a)速度Vが大きくなり、b)ストライドが大きくなり、c)ピッチは減少し、d)全体の仕事Wは極小値を迎えた。
滞空時間を短くする×θ₂一定だと、a)速度Vが大きくなり、b)ストライドは小さくなり、c）ピッチは増加し、d)全体の仕事Wは減少した。

ここから導きだせるのは、以下の事柄です。

所定の速度でランニングするときに、θ₂と滞空時間は固定ではなく、それらのバランスには一定の自由度がある。逆言えば、速度Vを決めても、θ₂と滞空時間は決まらない。
θ₂とストライドには強い相関性がある。ストライド走法とはθ₂を大きくすることで速度Vを増加させる走法である。
滞空時間とピッチには強い相関性がある。ピッチ走法とは滞空時間を短くすることで速度Vを増加させる走法である。

θ₂を大きくしても、滞空時間を短くしても、ともに速度Vを増加することが示されたことで、これまで何故、ストライド走法とピッチ走法の両方が存在し、決着がつかなかったのかが明確に示されました。しかし、両者の関係を紐解くことで、この議論にも終止符を打つことができます。

θ₂と滞空時間の組み合わせに対して、速度V、全体の仕事W、ストライドとピッチがどのように変化するかを示した。
所定の速度Vにおいて極小となる全体の仕事W_minを求めた。これにより、速度Vを増加させるためには、θ₂を増加させ、滞空時間は延長させることがわかった。このとき、ストライドは大きくなり、ピッチは減少する。

θ₂と滞空時間の組み合わせには自由度がある

そこで、θ₂と滞空時間の組み合わせに対して、速度V、ストライド、ピッチ、全体の仕事Wがどのように変化していくかを見てみましょう。θ₂を21°から40°と滞空時間を0.11sから0.21sまで、それぞれ変化させて、三次元のグラフを作成しました。

速度V

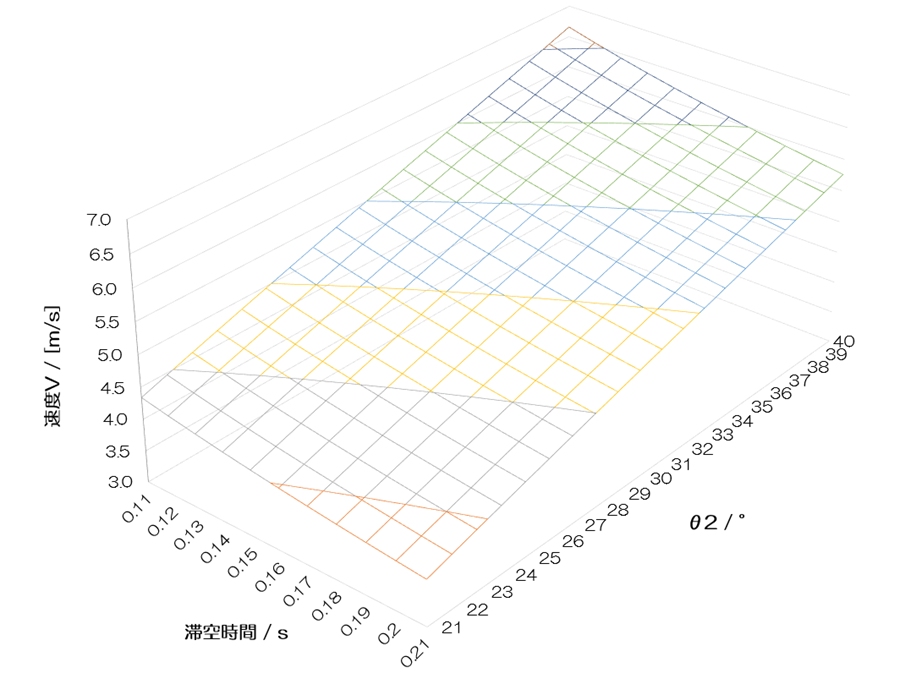
まず、速度Vのグラフです。平面であるように見えます。つまり、θ₂を増加させても線形に速度Vが増加し、滞空時間を短くしても速度Vが線形に増加することを示しています。滞空時間を短くすると速度Vが増加する、という結論は直感に反するかもしれません。

ストライド

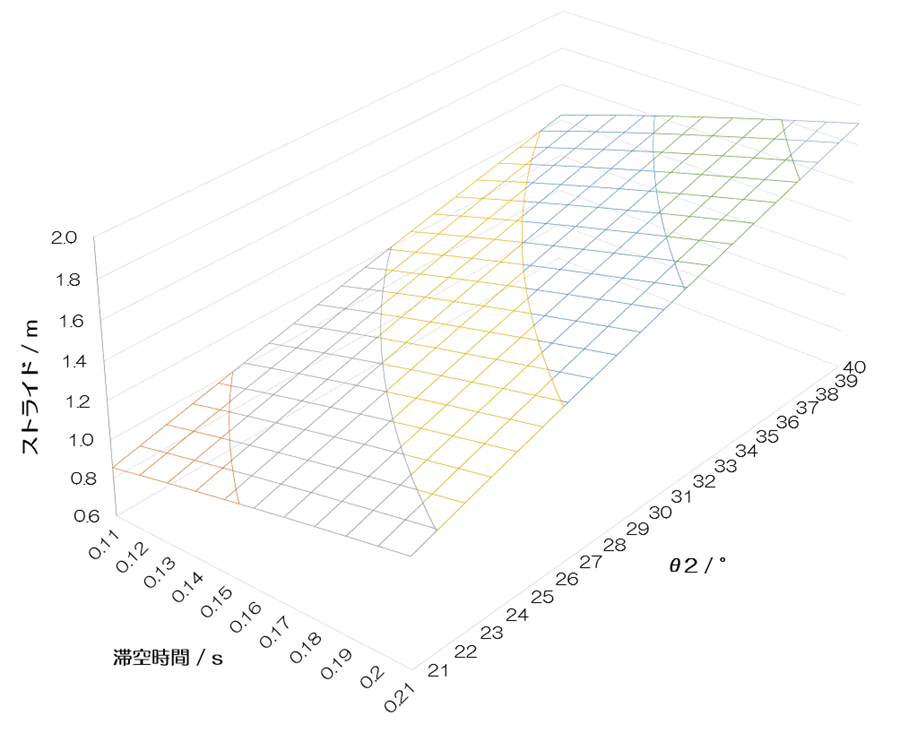
次にストライドのグラフを見てみましょう。θ₂が増加すると、ストライドが増加します。離地の瞬間における身体の傾きがθ₂ですから、これは意外ではありません。滞空時間が短縮すると、ストライドは減少しています。滞空時間が短縮すれば、滞空時に進む距離が減少しますから、ストライドが減少するのは当然です。

ピッチ

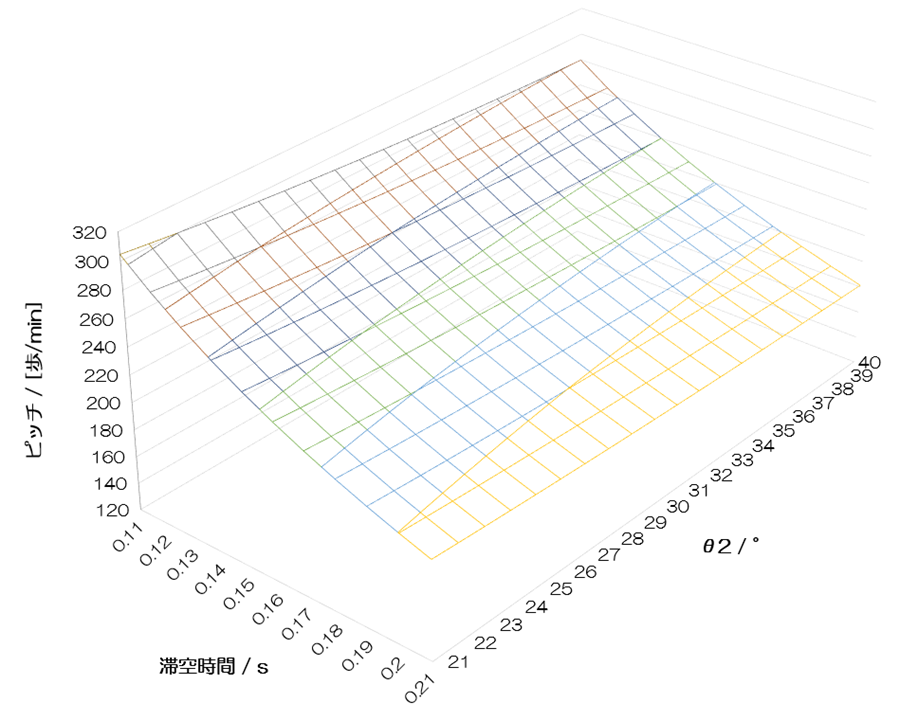
ピッチはどのように変化するでしょうか。これまで既に示されていたように、滞空時間を短縮すると、ピッチは明らかに増加します。240歩/minを超えた領域は現実的ではないと考えます。この辺りが、全体の仕事Wのグラフにどう表れてくるかに注目です。一方、θ₂との相関性は小さいですが、θ₂を増加させると、ピッチは減少します。

全体の仕事W

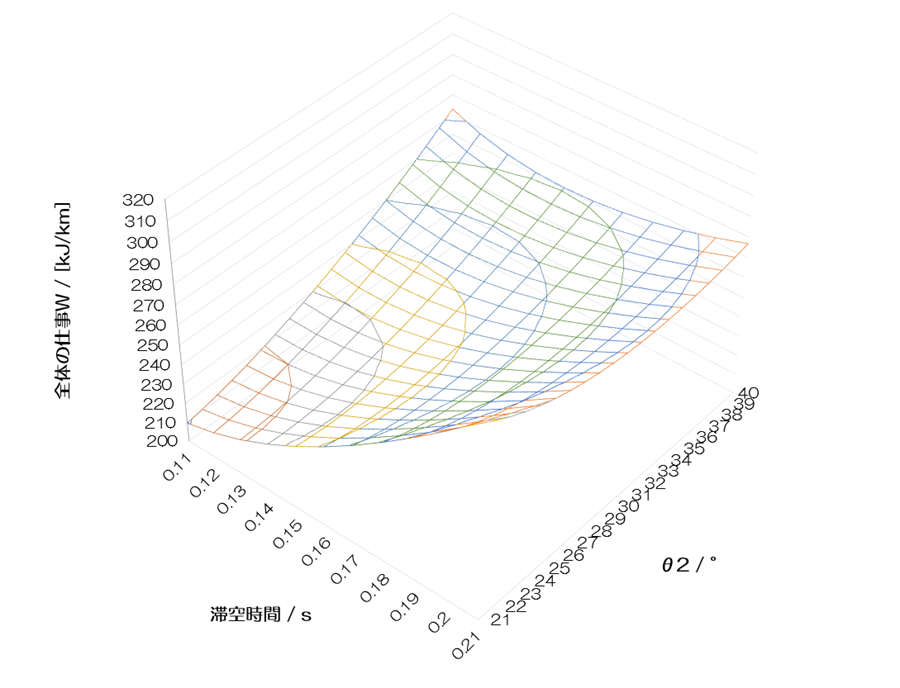
全体の仕事Wのグラフは特徴的です。大きく下向きに湾曲しています。今回見ている範囲においては、θ₂を一定にして、滞空時間を変化させていくと極小値を取ることを意味しています。滞空時間一定でθ₂を変化させたときはどうでしょうか。滞空時間0.11sのときには、見ている範囲には極小値はなさそうです。ところが、滞空時間0.21sのときには極小値がありそうです。

各速度における極小の全体の仕事W_minを求めてみた

ランニングの効率化とは、すなわち、所定の速度で走るための極小の全体の仕事W_minを見つけ出すことです。ここまでの検討では、θ₂と滞空時間に対して、速度V、ストライド、ピッチ、全体の仕事Wの変化を見てみましたが、実際に見たいのは、速度Vと全体の仕事Wの関係です。その関係がこれまで明らかでなかったのは、θ₂と滞空時間を変化させることにより、速度Vも変化し、全体の仕事Wも変化するためです。ところが、θ₂と滞空時間の組み合わせには一定の自由度があるために、速度Vと全体の仕事Wの関係性を見出すことができなかったのです。つまり、速度Vを指定してあげても、全体の仕事Wはわからなかったのです。

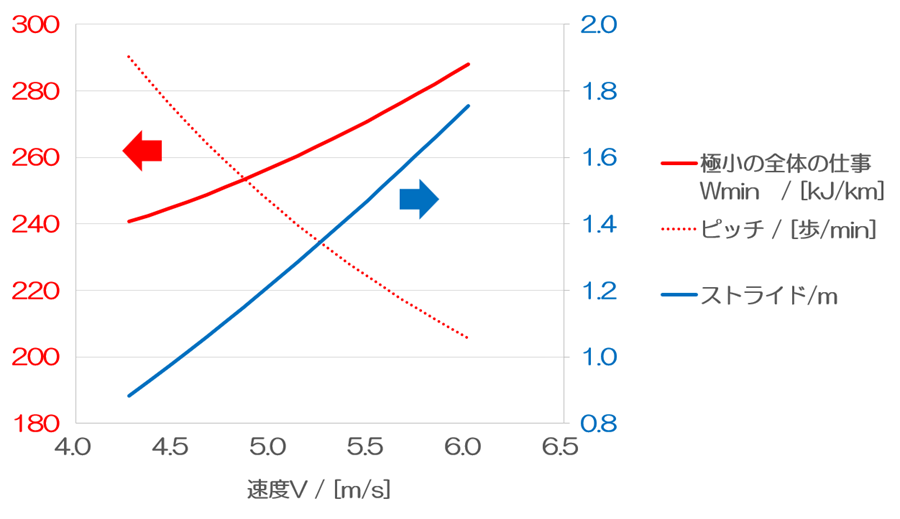
しかし、全体の仕事Wのグラフが可視化されたことで極小値を取ることがわかりました。私はランニングの最適化を追求していますから、興味があるのは、この極小値だけなのです。そこで、速度Vを変化させていき、各速度おける極小の全体の仕事W_min（赤線）を求めてみました。速度Vは横軸で示されています。速度Vが増加するに従い、極小の全体の仕事W_minは増加しました。これは、理に適った結論です。わざわざ言われなくても誰もが知っていることです。重要なのは、これに伴い、ストライドとピッチがどのように変わってくるか、です。

すると、下のようなグラフになります。速度Vが増加するに従い、ストライドが大きくなり、ピッチが減少していくことがわかります。極小の全体の仕事W_minを示す、θ₂と滞空時間の組み合わせにおいて、速度Vが増加して行くときは、ストライドが増加するものだと示されました。これは当然です。一方で、ストライドが増加する結果、ピッチは減少していきます。ピッチが減少することで、脚の入替にかかる仕事が減少するためです。ピッチは一定で、ストライドのみが増加するのではない、という点が私にとって意外な結果でした。

ただし、ストライドとピッチは意図的に変化させるものではなく、結果として変化するものです。意図的に変化させるのは、θ₂と滞空時間になります。下のグラフを見てみると、速度Vを増加させるためには、θ₂を増加させ、滞空時間も増加させるべきであるとわかります。重力ランニングの原則は、「接地中は加速することができるが、滞空中は減速するしかない」です。しかし、これを理解し、突き詰めたところで、出てきた結論が速度Vを増加させるときには、「θ₂を大きくし、滞空時間を長くする」だったのです。

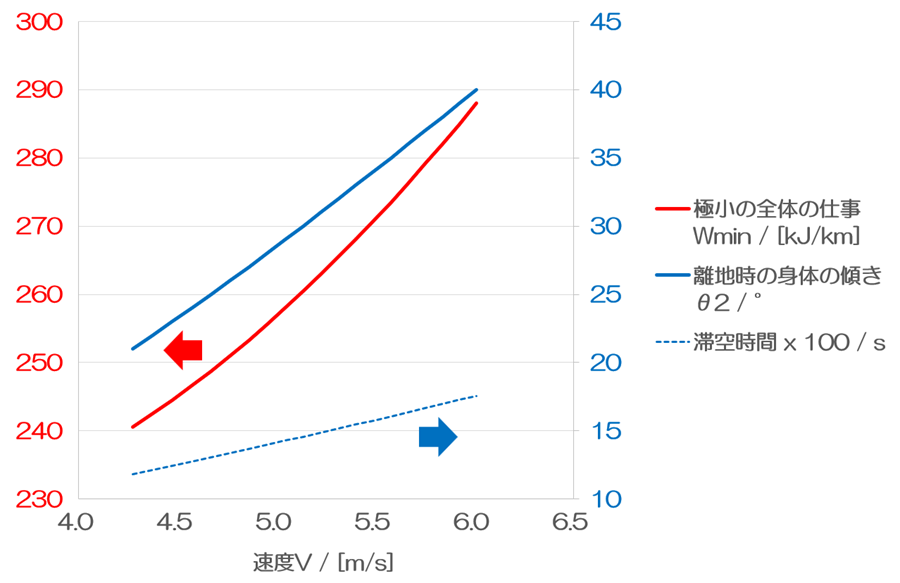
ただし、この命題が真であるのは、「極小の全体の仕事W_minを示す、θ₂と滞空時間の組み合わせが実現されている」ときです。これを実現するのが第一歩であり、速度Vの増加は次の段階です。そこで、次は、速度Vを一定に値に固定した上で、θ₂と滞空時間を変化させたときに、全体の仕事Wがどれくらい変化するのかを見てみます。