最適点からの逸脱の影響はいかに?重力ランニングのゆとり
前回の記事では、離地の瞬間の身体の傾きθ2と滞空時間の組み合わせを介して、速度Vと全体の仕事Wの関係性を明らかにしました。こうして、各速度Vにおける極小の全体の仕事Wを示しました。
これで重力ランニングの最適点はどこにあるのかを示しました。今回は、その最適点から離れるとどうなっていくのかを見ていきます。シミュレーションの仕方としては、速度Vを一定にし保ちながら、θ2と滞空時間のいずれかを最適点から離していきます。すると、全体の仕事Wは極小値から徐々に増加していくはずです。概念的には単純なのですが、速度Vを一定に保ちながら、θ2と滞空時間を変更するというプロセスが難しいのです。θ2と滞空時間を変更させて、その結果、速度Vがどうなるかを見るシミュレーションですので、θ2と滞空時間を変えた結果、速度Vが所望の値になるかどうかを繰り返すことになります。
- θ2と滞空時間を最適点からずらすことにより、全体の仕事Wが増加することを示した。
- 全体の仕事Wの増加率は最適点付近では小さいと考えられ、完全な合わせこみが行われずとも効率の良い走りができる。別の言い方をすれば、重力ランニングにおけるスイートスポットにはある程度の広さがある。
θ2と滞空時間と全体の仕事Wの関係を示す
時間はかかりましたが、一連の努力により、速度Vを4.0、4.5、5.0、5.5 m/sに保ちながら、θ2と滞空時間を変更させていきました。その結果が以下の表になります。
離地時の重心と接地点距離H:1.1 m100 mにおける比較
体重:60 ㎏
片脚の質量:6 ㎏
| 速度/[m/s] | θ2/° | 滞空時間/s | 全体の仕事W/[kJ/km] | ストライド/m | ピッチ/[歩/min] |
|---|---|---|---|---|---|
| 4.0 | 11 | 0.013 | 782 | 0.24 | 983 |
| 4.0 | 12 | 0.024 | 510 | 0.31 | 783 |
| 4.0 | 13 | 0.035 | 384 | 0.37 | 649 |
| 4.0 | 14 | 0.047 | 316 | 0.44 | 552 |
| 4.0 | 15 | 0.059 | 276 | 0.50 | 477 |
| 4.0 | 16 | 0.073 | 252 | 0.58 | 416 |
| 4.0 | 17 | 0.087 | 240 | 0.65 | 368 |
| 4.0 | 18 | 0.103 | 236 | 0.73 | 327 |
| 4.0 | 19 | 0.120 | 238 | 0.82 | 293 |
| 4.0 | 20 | 0.138 | 245 | 0.91 | 264 |
| 4.0 | 21 | 0.157 | 256 | 1.01 | 238 |
| 4.0 | 22 | 0.178 | 271 | 1.11 | 217 |
| 4.0 | 23 | 0.200 | 289 | 1.21 | 198 |
| 4.0 | 24 | 0.224 | 310 | 1.33 | 181 |
| 4.0 | 25 | 0.248 | 334 | 1.44 | 166 |
| 4.0 | 26 | 0.274 | 361 | 1.57 | 153 |
| 4.0 | 27 | 0.302 | 391 | 1.69 | 142 |
| 4.0 | 28 | 0.331 | 423 | 1.83 | 131 |
| 4.0 | 29 | 0.362 | 457 | 1.97 | 122 |
| 4.0 | 30 | 0.394 | 495 | 2.11 | 114 |
| 4.5 | 16 | 0.037 | 407 | 0.45 | 598 |
| 4.5 | 17 | 0.047 | 347 | 0.51 | 526 |
| 4.5 | 18 | 0.057 | 306 | 0.58 | 466 |
| 4.5 | 19 | 0.068 | 279 | 0.65 | 417 |
| 4.5 | 20 | 0.080 | 262 | 0.72 | 376 |
| 4.5 | 21 | 0.093 | 251 | 0.80 | 340 |
| 4.5 | 22 | 0.107 | 246 | 0.88 | 308 |
| 4.5 | 23 | 0.121 | 245 | 0.96 | 281 |
| 4.5 | 24 | 0.137 | 248 | 1.05 | 258 |
| 4.5 | 25 | 0.154 | 254 | 1.14 | 237 |
| 4.5 | 26 | 0.171 | 262 | 1.24 | 218 |
| 4.5 | 27 | 0.190 | 274 | 1.34 | 202 |
| 4.5 | 28 | 0.210 | 288 | 1.45 | 187 |
| 4.5 | 29 | 0.230 | 304 | 1.56 | 173 |
| 4.5 | 30 | 0.252 | 322 | 1.67 | 161 |
| 4.5 | 31 | 0.275 | 342 | 1.79 | 151 |
| 4.5 | 32 | 0.299 | 364 | 1.92 | 141 |
| 4.5 | 33 | 0.324 | 388 | 2.05 | 132 |
| 4.5 | 34 | 0.351 | 414 | 2.18 | 124 |
| 4.5 | 35 | 0.378 | 442 | 2.33 | 116 |
| 5.0 | 21 | 0.053 | 349 | 0.64 | 466 |
| 5.0 | 22 | 0.063 | 317 | 0.71 | 423 |
| 5.0 | 23 | 0.073 | 294 | 0.78 | 386 |
| 5.0 | 24 | 0.084 | 278 | 0.85 | 353 |
| 5.0 | 25 | 0.095 | 267 | 0.92 | 325 |
| 5.0 | 26 | 0.107 | 260 | 1.00 | 299 |
| 5.0 | 27 | 0.120 | 256 | 1.08 | 277 |
| 5.0 | 28 | 0.134 | 256 | 1.17 | 256 |
| 5.0 | 29 | 0.148 | 258 | 1.26 | 238 |
| 5.0 | 30 | 0.164 | 263 | 1.35 | 222 |
| 5.0 | 31 | 0.180 | 270 | 1.45 | 207 |
| 5.0 | 32 | 0.197 | 279 | 1.55 | 193 |
| 5.0 | 33 | 0.215 | 289 | 1.66 | 181 |
| 5.0 | 34 | 0.233 | 301 | 1.77 | 169 |
| 5.0 | 35 | 0.253 | 315 | 1.88 | 159 |
| 5.0 | 36 | 0.273 | 331 | 2.00 | 150 |
| 5.0 | 37 | 0.295 | 348 | 2.13 | 141 |
| 5.0 | 38 | 0.318 | 367 | 2.26 | 133 |
| 5.0 | 39 | 0.341 | 387 | 2.39 | 125 |
| 5.0 | 40 | 0.366 | 409 | 2.53 | 119 |
| 5.5 | 26 | 0.066 | 337 | 0.83 | 398 |
| 5.5 | 27 | 0.075 | 316 | 0.90 | 368 |
| 5.5 | 28 | 0.085 | 299 | 0.97 | 341 |
| 5.5 | 29 | 0.095 | 287 | 1.04 | 317 |
| 5.5 | 30 | 0.106 | 278 | 1.12 | 295 |
| 5.5 | 31 | 0.118 | 273 | 1.20 | 275 |
| 5.5 | 32 | 0.130 | 270 | 1.28 | 257 |
| 5.5 | 33 | 0.143 | 269 | 1.37 | 241 |
| 5.5 | 34 | 0.156 | 271 | 1.46 | 226 |
| 5.5 | 35 | 0.171 | 274 | 1.56 | 212 |
| 5.5 | 36 | 0.186 | 279 | 1.66 | 199 |
| 5.5 | 37 | 0.202 | 286 | 1.76 | 187 |
| 5.5 | 38 | 0.218 | 294 | 1.87 | 177 |
| 5.5 | 39 | 0.235 | 304 | 1.98 | 167 |
| 5.5 | 40 | 0.253 | 315 | 2.09 | 158 |
| 5.5 | 41 | 0.272 | 328 | 2.21 | 149 |
| 5.5 | 42 | 0.292 | 342 | 2.34 | 141 |
| 5.5 | 43 | 0.313 | 357 | 2.47 | 134 |
| 5.5 | 44 | 0.335 | 373 | 2.60 | 127 |
| 5.5 | 45 | 0.358 | 391 | 2.74 | 120 |
今回のデータから現象を理解するのが多少困難です。それは、各要素の因果関係が複雑だからです。例えば、速度Vが4.0 m/sのときの最適点から、θ2を変更すると速度Vが4.0 m/sでなくなってしまいます。そこで、速度Vが4.0 m/sになるように、滞空時間を調整します。こうして、速度Vが4.0 m/sに戻ります。そのとき、全体の仕事Wも算出されます。このような仕組みになっていますので、θ2と滞空時間の組み合わせに対して、全体の仕事Wの変化を示さなければなりません。しかし、それに適したグラフがありませんでしたので、θ2と全体の仕事Wの関係、滞空時間と全体の仕事Wの関係をそれぞれ示すことにします。
また、ピッチが異常に大きな値を示していると言わざるを得ません。速度Vが5.5 m/sのときに、ピッチが241歩/minですが、速度が小さくなるほどにピッチがさらに増加しています。
θ2をずらしたとき
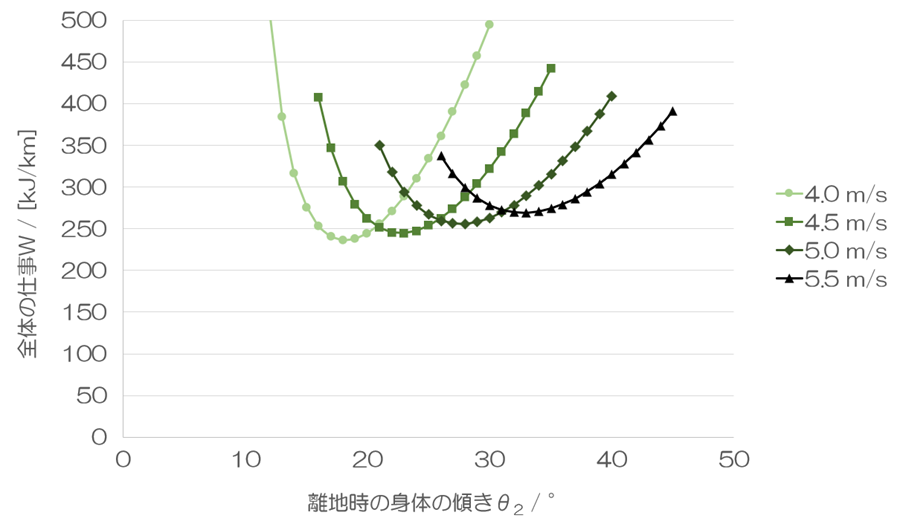
θ2を横軸に取り、縦軸に全体の仕事Wを取りました。最適点からθ2の値が前後に離れるとその分だけ、全体の仕事Wが増加します。θ2が減少すると滞空時間が短縮されるため、ピッチが増加し、全体の仕事Wが増加します。一方で、θ2が増加すると滞空時間が延長されるため、全体の仕事Wが増加します。このカーブは、速度Vが大きいほど緩やかになります。つまり、速い人ほど最適点からのずれの影響が小さいということです。ただし、速く走っている人は動きがそれだけ速いので、最適点への合わせこみは難しくなります。上記カーブの緩やかさを踏まえても、最適点の合わせこみは速度Vが大きいほど難しいというのが私の予想です。
滞空時間をずらしたとき
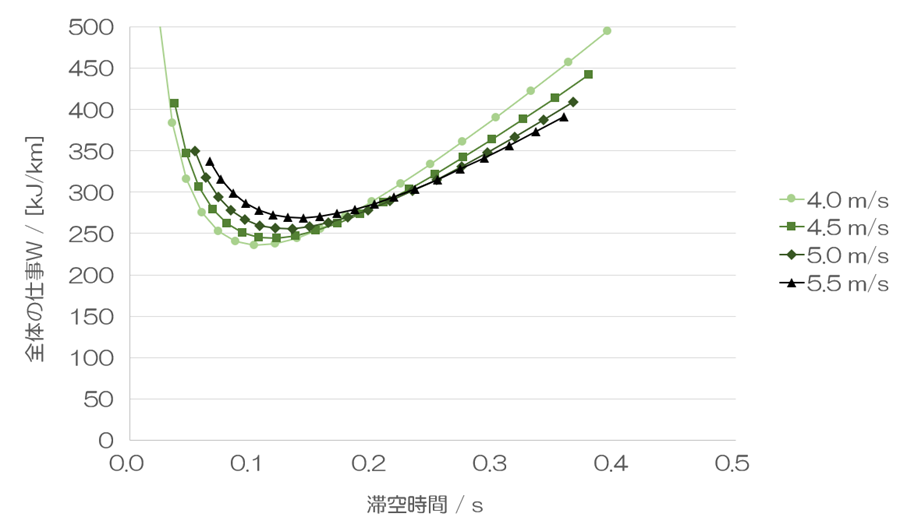
同様に、滞空時間を横軸に取った場合です。最適点から離れるほど、全体の仕事Wが大きくなるのは同じです。滞空時間が短くなるほどピッチが増加するというのは理解しやすいと思います。また、滞空時間が長くなるほど、身体の重心の上下動の範囲が広がるので、全体の仕事Wが増加するのも想像しやすいと思います。
これで、重力ランニングの目指す姿である最適点と、そこから逸脱したランニングの差を定量的に表現することができました。グラフの極小点の付近においては、グラフの傾きが小さくなるので、私の印象としては大体その辺りという感覚で良いのかな、という印象を持ちました。ただ、理解していただきたいのは、速度Vによって、θ2と滞空時間の両方が変わるということです。これに伴い、ピッチとストライドも両方とも変わります。レース中に速度を増加させるのであれば、最適点への合わせこみを行わなければならないのです。速度を増加させたけれども、ピッチは変わらず、ストライドだけ大きくなるという現象はあり得ないとは言いませんが、非効率なのです。レース終盤のスパートで、非効率なランニングに移行するのは、ぜひとも避けたいところです。
今回の議論では、最適点からの乖離の影響を見積もりましたが、具体的な値を見てみると、θ2と滞空時間の最適点においてもピッチが現実離れした大きな値となっています。この現象は、脚の質量に依存すると予想しています。次の記事では、その影響について調査します。