完全定常状態のシミュレーションで見えた本当の最適化
筋肉走りのモデル化の過程において、重力走りのモデルを見直すことになったというのは以下の記事で既に報告した通りです。
また、その後、筋肉走りのモデル化においては、重力ランニングと筋肉走りの身体重心の上下動をグラフで表現しています。しかし、そのグラフは一歩毎に、身体重心の軌跡が異なるというものでした。
一歩毎に次の一歩を計算した結果、こうなってしまったと正直に書いてあります。しかし、心の中では、モヤモヤした感覚を残していました。とにかく、筋肉走りと重力走りの違いを表現した後に、何をするかと考えたときに、このモヤモヤに立ち戻りました。つまり、一歩毎に身体重心の軌跡が変わらないシミュレーションを実現しようと考えました。
- 重力ランニングのシミュレーションの方法をさらに改善した。一歩の終わりが次の一歩の始まりとなるような、単独で繰り返し可能な1サイクルとしての一歩を導き出した。
- これにより、最適化されたランニングの様子を知ることができた。
完全な一歩のサイクルを構築する
シミュレーションの方法について記載します。今回の話は、物理モデルの話ではなく、そのモデルをどうEXCEL上で表現するかという話です。さすがに、ランニングとは関係ないので、ランニングに興味がある方は、次の節に進んでください。
従来のシミュレーションでは、時間t=0から0.01秒刻みで次のフレームを計算する、という考え方を原則に据えて、これを変えませんでした。したがって、θ2や滞空時間などのパラメータを変更する度に、どのフレームで離地し、どのフレームで着地するということが変わりました。これは、EXCELで集計するときに非常にやりにくいのです。ある一歩の最初から最後の情報を取りたいときに、どのセルを指定すれば良いかが決められないのです。また、歩数を重ねて行けば、ピッチやストライドなどが一定の値に収束すると予想していました。しかし、実際はそうはならず、一定の周期で変化を繰り返すような感じになりました。そこで、1フレームの時間を変化させることにしました。そして、接地区間を100フレーム、滞空区間を100フレームに分割して計算することにしました。これで、どのセルで接地区間が終わり、どのセルで滞空区間が終わるのかもわかります。これで、EXCEL上で必要な、条件設定などが行えるようになりました。
今までは、止まった状態から走り出して、定常状態に達するという考え方でしたが、これも捨てました。代わりに、完全な定常状態に達している一歩をシミュレートすることにしました。完全な定常状態に達しているとは、その一歩の終わりは、次の一歩の始まりとして完全に連続的につながるということです。接地の瞬間が一歩の終わりだと定義した場合、接地の瞬間が一歩の始まりです。したがって、接地区間の始まりである接地の瞬間の身体重心の高さと移動速度が、滞空区間の終わりである接地の瞬間において再出現しなければならないのです。これはあたかも、微分方程式を解くような作業です。よって、おおむね以下のような手順でシミュレーションの方法を開発しました。
- θ2と滞空時間の理論値を指定する。その後、1フレームの時間を接地区間と滞空区間でそれぞれ最適化することで、シミュレーション上のθ2と滞空時間を指定した値に一致させることができることを確認した。
- 最初のフレームと最後のフレームで、身体重心のX方向の速度Vx、Y方向の速度Vy、Y座標を一致させる条件を追加した。X座標を増加させるのが、ランニングであるから、X座標は成り行きで構わない。
新シミュレーションの結果
こうして、完全に定常状態の一歩を計算したものが以下です。
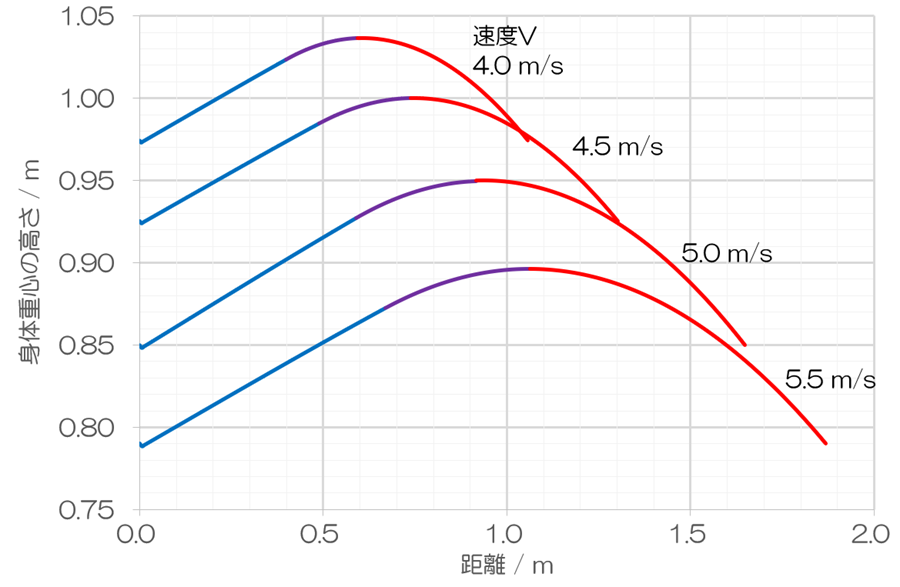
グラフの形は、従来のものと大きく変わっていません。しかし、最も重要な違いは、グラフの始点と終点において、重心の高さが同じになっている点です。従来のシミュレーションでは、これが一致していませんでした。
| 速度V / [m/s] | 4.0 | 4.5 | 5.0 | 5.5 |
|---|---|---|---|---|
| 実際の離地時の身体の傾きθ2 / ° | 21 | 26 | 32 | 37 |
| 実際の滞空時間 / s | 0.17 | 0.18 | 0.21 | 0.22 |
| ストライド / m | 1.06 | 1.30 | 1.65 | 1.87 |
| ピッチ / [歩/min] | 227 | 208 | 182 | 177 |
| 重心の移動の仕事W1/[kJ/km] | 174.2 | 183.1 | 203.6 | 209.6 |
| 脚の入替の仕事W2/[kJ/km] | 83.4 | 81.5 | 75.5 | 78.5 |
| 全体の仕事W / [kJ/km] | 257.5 | 264.6 | 279.2 | 288.1 |
| 身体の重心の接地時の高さh0/m | 0.974 | 0.925 | 0.850 | 0.790 |
| 身体の重心の離地時の高さh1/m | 1.023 | 0.984 | 0.926 | 0.871 |
| 身体の重心の高さの最大値hmax/m | 1.036 | 1.000 | 0.950 | 0.896 |
従来の結果と比較して、全体の仕事Wは良い一致を見せていると考えます。今回の方法においては、狙い通り、モデル自体は変えずに、計算方法をだけを変えることで、シミュレーションの精度だけを高めることに成功しました。
この結果は、完全な定常状態における一歩ですので、細かいところを比較する意味も出てきます。hmaxとh0の差は、ランニング中の身体重心の上下動の幅を表しています。速度が大きくなるほど、ランニング中の上下動の幅は大きくなります。4.0 m/sにおいて0.062 mから、5.5 m/sにおいて0.106 m/sと変化しています。物理量としては小さな値です。しかし、全てを効率化した重力ランニングにおいては、身体重心の上下動が最終的に残された無駄な労力ですので、大きな意味を持ちます。ランニングは身体重心を前方に移動させるのが目的という前提において、目的達成には全く関係のない身体重心の上下動を抑えようとしても、最小限、これくらいは残ってしまうということです。
今回の記事では、読者の皆さまにとっては新しい発見はほとんどないかも知れません。しかし、細かい解析に対して不便さの残る方法では、この先の研究が続けられないと思っていたので、一定の改善ができて、自分としては安心しました。


